题目内容
【题目】如图,△ABC是边长为8的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(点Q不与点B重合),过P作PE⊥AB于E,连接PQ交AB于D,在运动的过程中线段ED的长为( )
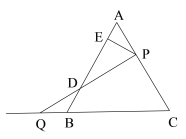
A.1.5B.2C.3D.4
【答案】D
【解析】
过点P作PF∥BC,先证明△APF是等边三角形,利用PE⊥AB得到AE=FE,再证明△PFD≌△QBD得到FD=BD,由此即可得到DE=![]() AB=4.
AB=4.
过点P作PF∥BC,
∵△ABC是等边三角形,
∴∠ABC=∠C=∠A=60°,
∵PF∥BC,
∴∠AFP=∠ABC=∠C=∠APF=60°,
∴△APF是等边三角形,
∴AP=FP,
∵PE⊥AB,
∴AE=FE,
∵点P、Q的运动速度相同,同时开始运动,
∴BQ=AP=FP,
∵PF∥BC,
∴∠PFD=∠QBD,
在△PFD和△QBD中
 ,
,
∴△PFD≌△QBD,
∴FD=BD,
∴FD+EF=BD+AE,
∴DE=![]() AB=4,
AB=4,
故选:D.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目