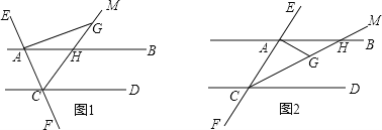题目内容

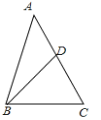
【题目】如图，在△ABC中，AB＝AC，AD和BE是高，它们相交于点H，且AE＝BE

求证：AH＝2BD

【答案】详见解析

【解析】

由等腰三角形的底边上的垂线与中线重合的性质求得BC=2BD，根据直角三角形的两个锐角互余的特性求知∠1+∠C=90°；又由已知条件AE⊥AC知∠2+∠C=90°，所以根据等量代换求得∠1=∠2；然后由三角形全等的判定定理SAS证明△AEH≌△BEC，再根据全等三角形的对应边相等及等量代换求得AH=2BD

∵AD是高,BE是高

∴∠EBC+∠C=∠CAD+∠C=90°

∴∠EBC=∠CAD

又∵AE＝BE

∠AEH=∠BEC

∴△AEH△BEC(ASA)

∴AH ＝BC

∵AB＝AC，AD是高

∴BC=2BD

∴AH ＝2BD

练习册系列答案
相关题目

【题目】某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶，然后以每瓶6元的价格出售，如果当天卖不完，剩余的只有倒掉．店主记录了30天的日需求量（单位：瓶），整理得下表：

（1）求这30天内日需求量的众数；

（2）假设鲜奶店在这30天内每天购进28瓶，求这30天的日利润（单位：元）的平均数；

（3）以30记录的各需求量的频率作为各需求是发生的概率．若鲜奶店每天购进28瓶，求在这记录的30天内日利润不低于81元的概率．

【题目】反比例函数y=（k为常数，且k≠0）的图象经过点A（1，3）、B（3，m）．

（1）求反比例函数的解析式及B点的坐标；

（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

【题目】小明从家出发沿滨江路到外滩公园徒步锻炼，到外滩公园后立即沿原路返回，小明离开家的路程s（单位：千米）与走步时间t（单位：小时）之间的函数关系如图所示，其中从家到外滩公园的平均速度是4千米/时，根据图形提供的信息，解答下列问题：

（1）求图中的a值；

（2）若在距离小明家5千米处有一个地点C，小明从第一层经过点C到第二层经过点C，所用时间为1.75小时，求小明返回过程中，s与t的函数解析式，不必写出自变量的取值范围；

（3）在（2）的条件下，求小明从出发到回到家所用的时间．

【题目】如图，等腰△ABC中，AB＝AC＝10cm，BC＝12cm，D为BC上一点，连接AD，E为AD上一点，连接BE，若∠ABE＝∠BAE═∠BAC，则DE的长为（ ）

A.cmB.cmC.cmD.1cm

【题目】如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A(3，0)、B(0，4)，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．

（1）求直线AB的表达式；

（2）求点C和点D的坐标；

（3）y轴的正半轴上是否存在一点P，使得S△PAB＝S△OCD？若存在，求出点P的坐标；若不存在，请说明理由．

【题目】在△ABC中，AB=AC，DB为△ABC的中线，且BD将△ABC周长分为12cm与15cm两部分，求三角形各边长．

【题目】如图，分别是数轴上四个整数所对应的点，其中有一点是原点，并且这四个整数点每相邻两点之间的距离为1个单位长度．数对应的点在与之间，数对应的点在与之间．若，则原点是（ ）

A.或B.与C.与D.与

【题目】已知直线AB∥CD，直线EF分别交AB、CD于A、C，CM是∠ACD的平分线，CM交AB于H，过A作AG⊥AC交CM于G．

（1）如图1，点G在CH的延长线上时，

①若∠GAB=36°，则∠MCD=______．

②猜想：∠GAB与∠MCD之间的数量关系是______．

（2）如图2，点G在CH上时，（1）②猜想的∠GAB与∠MCD之间的数量关系还成立吗？如果成立，请给出证明；如果不成立，请写出∠GAB与∠MCD之间的数量关系，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网