题目内容
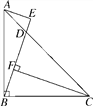
【题目】如图，等腰△ABC中，AB＝AC＝10cm，BC＝12cm，D为BC上一点，连接AD，E为AD上一点，连接BE，若∠ABE＝∠BAE═
∠BAC，则DE的长为（ ）
A.
cmB.
cmC.
cmD.1cm
【答案】C
【解析】
先根据等腰三角形三线合一的性质得：AD⊥BC，及BD的长，利用勾股定理计算AD的长，设DE＝x，则AE＝BE＝8﹣x，在Rt△BDE中利用勾股定理列方程可解答．
解：∵AB＝AC，∠BAE═
∠BAC，
∴AD⊥BC，
∴∠BDE＝90°，BD＝BC＝6，
∵AB＝10，
∴AD＝
＝8，
∵∠ABE＝∠BAE，
∴AE＝BE，
设DE＝x，则AE＝BE＝8﹣x，
在Rt△BDE中，BE2＝DE2+BD2，
∴（8﹣x）2＝x2+62，
解得：x＝
，
即DE＝cm，
故选：C．
练习册系列答案
相关题目
【题目】已知一圆形零件的标准直径是
，超过规定直径长度的数量(毫米)记作正数，不足规定直径长度的数量(毫米)记作负数，检验员某次抽查了零件样品，检查的结果如下：
序号 |
|
|
|
|
|
直径长度/ |
|
|
|
|
|
（1）试指出哪件样品的大小最符合要求？
（2）如果规定误差的绝对值在
之内是正品.误差的绝对值在
之间是次品，误差的绝对值超过
的是废品，那么上述五件样品中，哪些是正品，哪些是次品，哪些是废品？
