题目内容
【题目】已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.
(1)如图1,点G在CH的延长线上时,
①若∠GAB=36°,则∠MCD=______.
②猜想:∠GAB与∠MCD之间的数量关系是______.
(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.
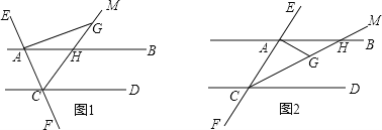
【答案】(1)①63°;②2∠MCD-∠GAB=90°;(2)2∠MCD+∠GAB=90°,理由见解析.
【解析】
(1)①依据AG⊥AC,∠GAB=36°,可得∠CAH的度数,依据角平分线的定义以及平行线的性质,即可得到∠MCD的度数;
②设∠ACH=∠AHC=∠MCD=α,∠GAB=β,则∠AGC=∠AHC-∠GAB=α-β,依据Rt△ACG中,∠ACH+∠AGC=90°,即可得出∠GAB与∠MCD之间的数量关系;
(2)设∠ACH=∠AHC=∠MCD=α,∠GAB=β,则∠AGC=∠AHC+∠GAB=α+β,依据Rt△ACG中,∠ACH+∠AGC=90°,即可得出∠GAB与∠MCD之间的数量关系.
解:(1)①∵AG⊥AC,∠GAB=36°,
∴∠CAH=90°-36°=54°,
∵AB∥CD,
∴∠ACD=180°-∠CAH=126°
∵CM是∠ACD的平分线,
∴∠MCD=![]() ∠ACD=63°,
∠ACD=63°,
故答案为:63°;
②∠GAB与∠MCD之间的数量关系是2∠MCD-∠GAB=90°;
理由:∵CM是∠ACD的平分线,
∴∠ACH=∠DCM,
∵AB∥CD,
∴∠AHC=∠DCM,
∴∠ACH=∠AHC,
设∠ACH=∠AHC=∠MCD=α,∠GAB=β,
则∠AGC=∠AHC-∠GAB=α-β,
∵GA⊥AC,
∴Rt△ACG中,∠ACH+∠AGC=90°,即α+α-β=90°,
∴2α-β=90°,即2∠MCD-∠GAB=90°;
故答案为:2∠MCD-∠GAB=90°;
(2)上述∠GAB与∠MCD之间的数量关系不成立,应该为2∠MCD+∠GAB=90°,
理由:∵CM是∠ACD的平分线,
∴∠ACH=∠DCH,
∵AB∥CD,
∴∠AHC=∠DCH,
∴∠ACH=∠AHC,
设∠ACH=∠AHC=∠MCD=α,∠GAB=β,
则∠AGC=∠AHC+∠GAB=α+β,
∵GA⊥AC,
∴Rt△ACG中,∠ACH+∠AGC=90°,即α+α+β=90°,
∴2α+β=90°,即2∠MCD+∠GAB=90°