题目内容
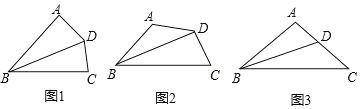
【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
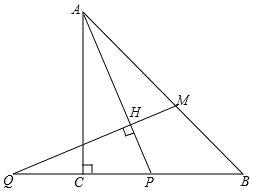
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
【答案】(1)角平分线上的点到角的两边距离相等;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据角平分线的性质定理解答;
(2)作 DE⊥BA 交 BA 延长线于 E,DF⊥BC 于 F,证明△DEA≌△DFC,根据全等三角形的性质证明;
(3)在 BC 时截取 BK=BD,连接 DK,根据(2)的结论得到 AD=DK,根据等腰三角形的判定定理得到 KD=KC,结合图形证明.
解:(1)∵BD 平分∠ABC,∠BAD=90°,∠BCD=90°,
∴DA=DC(角平分线上的点到角的两边距离相等),
故答案为:角平分线上的点到角的两边距离相等;
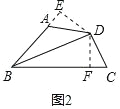
(2)如图 2,作DE⊥BA 交 BA延长线于 E,DF⊥BC 于 F,
∵BD 平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
在△DEA 和△DFC 中,
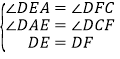
∴△DEA≌△DFC(AAS),
∴DA=DC;
(3)如图,在 BC 时截取 BK=BD,连接 DK,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD 平分∠ABC,
∴∠DBK=![]() ∠ABC=20°,
∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,即∠A+∠BKD=80°, 由(2)的结论得 AD=DK,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∴AD=DK=CK,
∴BD+AD=BK+CK=BC.