题目内容
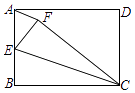
【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 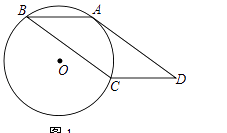
(1)求证:弧AB=弧AC
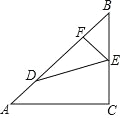
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 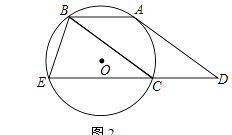
【答案】
(1)证明:证明:连接OA交BC于F.
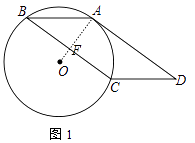
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分 ![]() ,
,
即 ![]() =
= ![]() .
.
(2)解:如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.
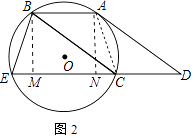
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BE=AB=AC, ![]() =
= ![]() ,
,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,
,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,
,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠D= ![]() .
.
【解析】(1.)如图1中,连接OA交BC于F.只要证明OF⊥BC即可解决问题. (2.)如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.首先证明BE=AB=AC, ![]() =
= ![]() ,推出∠E=∠ACE,在Rt△BEM中,sin∠E=
,推出∠E=∠ACE,在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E=
,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE=
,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE= ![]() =
= ![]() =
= ![]() ,可得tan∠D=
,可得tan∠D= ![]() .
.
【考点精析】掌握平行四边形的性质和切线的性质定理是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.