题目内容
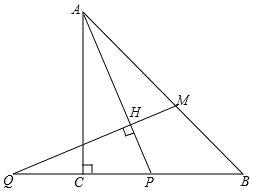
【题目】如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点 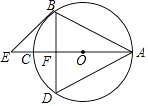
(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
【答案】
(1)解:如图,连接CD、OD、BO,延长BO交AD于点G,
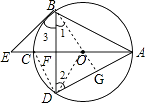
在△ABO和△DBO中,
∵ 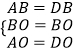 ,
,
∴△ABO≌△DBO(SSS),
∴∠1=∠ABO,
∴BG⊥AD,
∴∠1+∠2=90°,
∵BE∥AD,
∴∠2=∠3,
∴∠3+∠1=90°,即OB⊥BE,
∴BE为⊙O的切线
(2)解:设CF=x,则AF=4x,
∴AC=5x,OC=OB= ![]() AC=
AC= ![]() x,
x,
∴OF=OC﹣CF= ![]() x﹣x=
x﹣x= ![]() x,
x,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴CD∥BG,
∴△CDF∽△OBF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
则CD= ![]() x,
x,
∴AD= ![]() =
= ![]() =
= ![]() x,
x,
∵BE∥AD,
∴tanE=tan∠CAD= ![]() =
= ![]() =
= ![]()
【解析】(1)连接CD、OD、BO,延长BO交AD于点G,证△ABO≌△DBO得∠1=∠ABO,从而得BG⊥AD,即∠1+∠2=90°,根据∠2=∠3知∠3+∠1=90°,得证;(2)设CF=x,则AF=4x、OC=OB= ![]() AC=
AC= ![]() x、OF=OC﹣CF=
x、OF=OC﹣CF= ![]() x,证△CDF∽△OBF得
x,证△CDF∽△OBF得 ![]() =
= ![]() ,从而求得CD=
,从而求得CD= ![]() x、AD=
x、AD= ![]() =
= ![]() x,由tanE=tan∠CAD=
x,由tanE=tan∠CAD= ![]() 可得答案.
可得答案.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
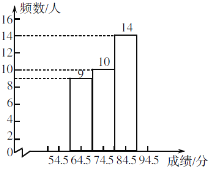
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.