题目内容
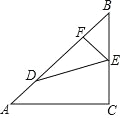
【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是G,且点G在边AD上,若EG⊥AC,AB=2,则FG的长为 . 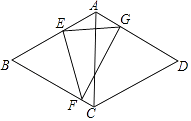
【答案】![]()
【解析】解:∵四边形ABCD是菱形,∠BAD=120°, ∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD是等边三角形,
∵EG⊥AC,
∴∠AEG=∠AGE=30°,
∵∠B=∠EGF=60°,
∴∠AGF=90°,
∴FG⊥BC,
∴2S△ABC=BCFG,
∴2× ![]() ×(2)2=2FG,
×(2)2=2FG,
∴FG= ![]() .
.
故答案为 ![]() .
.
首先证明△ABC,△ADC都是等边三角形,再证明FG是菱形的高,根据2S△ABC=BCFG即可解决问题.

练习册系列答案
相关题目