题目内容
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象. 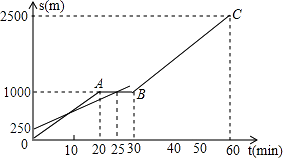
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
【答案】
(1)解:设小明所走路程s与时间t的函数关系式为s=kt+b(k≠0),
当0≤t≤20时,将点(20,1000)、(0,0)代入s=kt+b,
得: ![]() ,解得:
,解得: ![]() ,
,
∴s=50t;
当20≤t≤30时,s=1000;
当30≤t≤60时,将(30,1000)、(60,2500)代入s=kt+b,
得: ![]() ,解得:
,解得: ![]() ,
,
∴s=50t﹣500.
综上所述:小明所走路程s与时间t的函数关系式为s= 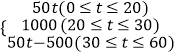
(2)解:爸爸的速度为(1000﹣250)÷25=30(m/min),
∴爸爸所走路程s与小明出发时间t的函数关系式为s=30t+250.
令s=30t+250=50t﹣500,
解得:t=37.5.
答:小明出发37.5min与爸爸第三次相遇.
(3)解:当s=30t+250=2500时,t=75,
∵75﹣60=15(min),
∴若小明比爸爸早20min到达公园,则小明在步行过程中停留的时间应缩短为5min.
【解析】(1)分0≤t≤20、20≤t≤30以及30≤t≤60三段,根据点的坐标,利用待定系数法求出函数关系式;(2)先求出爸爸所走路程s与小明出发时间t的函数关系式,再令其等于s=50t﹣500,解之即可求出二者第三次相遇的时间;(3)根据一次函数图象上点的坐标特征可求出爸爸到达公园的时间,根据它与60之间的关系,调整小明中途休息时间即可.

 名校课堂系列答案
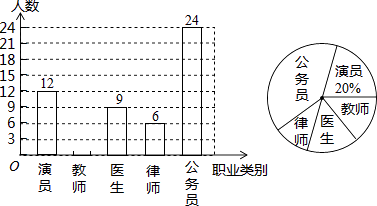
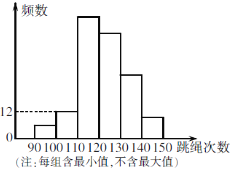
名校课堂系列答案【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
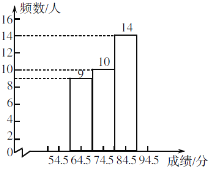
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.