Question

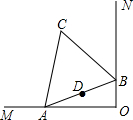
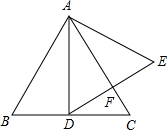
如图，在等边三角形ABC中，AD⊥BC于点D，以AD为一边向右作等边三角形ADE，DE与AC交于点F．
（1）试判断DF与EF的数量关系，并给出理由．
（2）若CF的长为2cm，试求等边三角形ABC的边长．

Answer 1

（1）DF=EF．
理由：∵△ABC和△ADE均是等边三角形，
∴∠BAC=∠DAE=60°，
∵AD⊥BC，
∴BD=DC，∠BAD=∠DAC=

1

2

×60°=30°，
∴∠CAE=60°-30°=30°，
即∠DAC=∠CAE，
∴AC垂直平分DE，
∴DF=EF；

（2）在Rt△DFC中，∵∠FCD=60°，∠CFD=90°，
∴∠CDF=90°-60°=30°，
∵CF=2cm，
∴DC=4cm，
∴BC=2DC=2×4=8cm，
即等边三角形ABC的边长为8cm．