Question

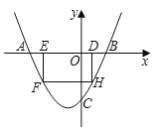
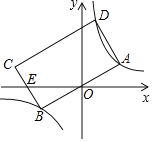
【题目】如图，矩形ABCD的顶点A，B，D分别落在双曲线y＝（k＞0）的两个分支上，AB边经过原点O，CB边与x轴交于点E，且EC＝EB，若点A的横坐标为1，则矩形ABCD的面积_____．

Answer 1

【答案】．

【解析】

过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N，过点A作AF⊥x轴于点F，设A点坐标为（1，a），则OB、BE、EM均可用a表示，易知△CNE≌△BME，通过线段等量关系可求用a表示的C点坐标，继而求得D点坐标，根据A、D都在反比例函数图象上，得到关于a的方程，求解a值，再求出AB和BC值，则矩形面积可求．

设A点坐标为(1，a)，过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N，过点A作AF⊥x轴于点F，如下图所示，

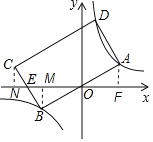
由A(1，a)，

由对称性质有B(﹣1，﹣a)，BM＝AF＝a，OM＝OF＝1，

∴OB＝OA＝，

∵tan∠BOE＝tan∠AOF，

∴，即，

∴BE＝，

∴，

∵BE＝CE，∠CEN＝∠BEM，∠CNE＝∠BME，

∴△CNE≌△BME，

∴CN＝BM＝a，NE＝EM＝a2，CE＝BE＝，

∴ON＝2a2+1，

∴C(﹣2a2﹣1，a)，

∵A(1，a)，B(﹣1，﹣a)，BC//AD，AD＝BC，

∴D(1﹣2a2，3a)，

∵A、D都在反比例函数图象上，

∴3a(1﹣2a2)＝a1，

解得a＝，

∴AB＝2OA＝2＝，BC＝2BE＝2a＝，

∴矩形ABCD的面积 ．

故答案为：．