题目内容
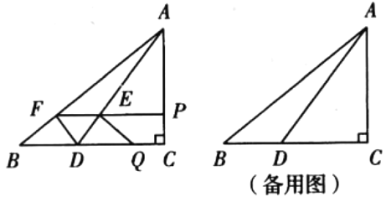
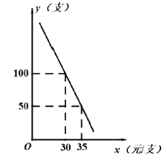
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
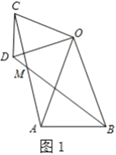
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
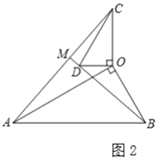
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
【答案】(1)证明见解析;![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)证明△COA≌△DOB(SAS),得AC=BD,;由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理得:∠AMB=180°﹣(∠DBO+∠OAB+∠ABD)=40°;
(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则![]() ,由全等三角形的性质得∠AMB的度数;
,由全等三角形的性质得∠AMB的度数;
(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC∽△BOD,则∠AMB=90°,![]() ,可得AC的长.
,可得AC的长.
解:(1)问题发现
如图1,∵∠AOB=∠COD=40°,
∴∠COA=∠DOB,
∵OC=OD,OA=OB,
∴△COA≌△DOB(SAS),
∴AC=BD;
∵△COA≌△DOB,
∴∠CAO=∠DBO,
∵∠AOB=40°,
∴∠OAB+∠ABO=140°,
在△AMB中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD)=180°﹣(∠DBO+∠OAB+∠ABD)=180°﹣140°=40°,
∴![]() ,
,
(2)类比探究
如图2,
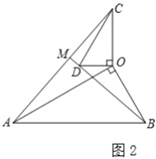
![]() ,∠AMB=90°,理由是:
,∠AMB=90°,理由是:
Rt△COD中,∠DCO=30°,∠DOC=90°,
∴![]() ,
,
同理得:![]() ,
,
∴![]() ,
,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
∴△AOC∽△BOD,
∴![]() ,∠CAO=∠DBO,
,∠CAO=∠DBO,
在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°;
(3)拓展延伸
①点C与点M重合时,如图3,
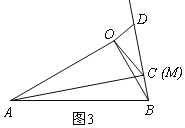
同理得:△AOC∽△BOD,
∴∠AMB=90°,![]() ,
,
设BD=x,则AC=![]() x,
x,
Rt△COD中,∠OCD=30°,OD=1,
∴CD=2,BC=x﹣2,
Rt△AOB中,∠OAB=30°,OB=![]() ,
,
∴AB=2OB=2![]() ,
,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
![]() ,
,
x2﹣x﹣6=0,
(x﹣3)(x+2)=0,
x1=3,x2=﹣2,
∴AC=3![]() ;
;
②点C与点M重合时,如图4,
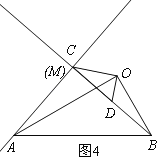
同理得:∠AMB=90°,![]() ,
,
设BD=x,则AC=![]() x,
x,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
![]() ,
,
x2+x﹣6=0,
(x+3)(x﹣2)=0,
x1=﹣3,x2=2,
∴AC=2![]() ;
;
综上所述,AC的长为3![]() 或2
或2![]() .
.

【题目】如图1,![]() ,
,![]() ,
,![]() 是郑州市二七区三个垃圾存放点,点
是郑州市二七区三个垃圾存放点,点![]() ,
,![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向,![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 丁 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列间不完整的统计图2.
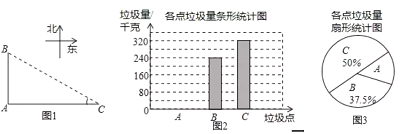
(1)表中的中位数是 、众数是 ;
(2)求表中![]() 长度的平均数
长度的平均数![]() ;
;
(3)求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
(4)用(2)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.