题目内容
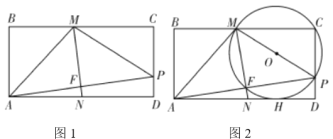
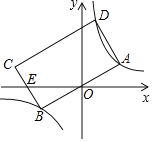
【题目】已知,如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
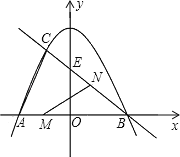
(1)求直线![]() 的解析式:
的解析式:
(2)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从点
上以每秒1个单位长度的速度从点![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 、
、![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从点
上以每秒2个单位长度的速度从点![]() 向点
向点![]() 方向运动,设运动的时间为
方向运动,设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 取何值时,
取何值时,![]() 最大?最大值是多少?
最大?最大值是多少?
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 秒时,
秒时,![]() 最大,最大值是
最大,最大值是![]() .
.
【解析】
(1)先利用抛物线求出点B的坐标,再将点B坐标代入直线BC的函数解析式即可求得b的值,进而得到BC的函数解析式;
(2)过点N作NF⊥x轴于点F,先证![]() ,再利用相似三角形的性质可表示出NF,根据S△MNB=
,再利用相似三角形的性质可表示出NF,根据S△MNB=![]() BM×NF,可求出S与t的函数关系式,利用配方法可求出最大值.
BM×NF,可求出S与t的函数关系式,利用配方法可求出最大值.
解:(1)在![]() 中,令
中,令![]() ,
,
可得![]() ,
,
解得![]() ,
,![]() .
.
![]() ,
,![]() .
.
又![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() .
.
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
(2)将![]() 代入
代入![]() 中,
中,
可得![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
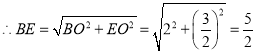 .
.
如图,过点![]() 作
作![]() 于点F,
于点F,
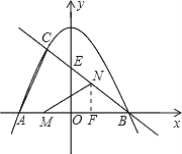
![]() ,
,![]() ,
,
∴EO∥NF,
![]() ,
,
![]() .
.
![]() ,
,
 ,
,
![]() .
.
∵AM=t,
∴![]() ,
,
![]()
![]()
![]() ,
,
即![]() .
.
![]() ,
,
![]() 抛物线开口向下,
抛物线开口向下,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 最大
最大![]() .
.
![]() 当
当![]() 秒时,
秒时,![]() 最大,最大值是
最大,最大值是![]() .
.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
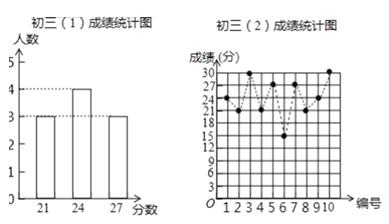
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下:
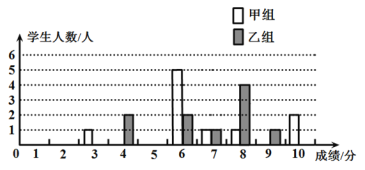
(1)将下表补充完整:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 | 6.8 |
| 6 | 3.96 | 90% | 20% |
乙 |
| 7.5 |
| 2.76 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生(填“甲””或“乙”);
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.