题目内容
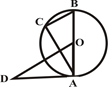
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC//OD,AB=2,OD=3,则BC的长为( )

A. | B. | C.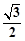 | D. |
A
试题分析:根据圆周角定理可得∠C=90°,根据切线的性质可得∠OAD=90°,根据平行线的性质可得∠B=∠DOA,即可证得△OAD∽△BCA,最后根据相似三角形的性质求解即可.
∵AB是⊙O的直径,AD是⊙O的切线
∴∠C=90°,∠OAD=90°
∵BC//OD
∴∠B=∠DOA
∴△OAD∽△BCA
∴
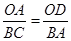
∵AB=2,OD=3
∴
 ,解得
,解得
故选A.
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中半径常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
 长为
长为 .
.
 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;
 的直径,点C是半圆的中点,动点P在弦BC上,则
的直径,点C是半圆的中点,动点P在弦BC上,则 可能为( )
可能为( )

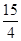 ,以O为圆心,OA为半径作圆.
,以O为圆心,OA为半径作圆.
 的三等分点,
的三等分点,  ,则
,则 的度数为 .
的度数为 . 