题目内容
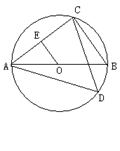
如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于点F。
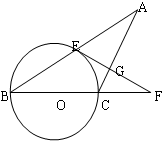
(1)求证:AE=BE
(2)求证:FE是⊙O的切线
(3)若BC=6,FE=4,求FC和AG的长。

(1)求证:AE=BE
(2)求证:FE是⊙O的切线
(3)若BC=6,FE=4,求FC和AG的长。
(1)连接EC,根据BC为⊙OD 的直径可得CE⊥AB,再由AC=BC根据等腰三角形三线合一的性质即可证得结论;(2)连接OE,根据三角形的中位线定理可得OE∥AC,再结合EG⊥AC即可证得OE⊥EF,从而证得结论;(3)CF=2,

试题分析:(1)连接EC,根据BC为⊙OD 的直径可得CE⊥AB,再由AC=BC根据等腰三角形三线合一的性质即可证得结论;
(2)连接OE,根据三角形的中位线定理可得OE∥AC,再结合EG⊥AC即可证得OE⊥EF,从而证得结论;
(3)由BC=2OE=6可得OE=3,再根据勾股定理可求得OF=5,即得CF=2,由OE∥AC可得△FCG∽△FEO,根据相似三角形的性质可求得CG的长,从而求得结果.
(1)连接EC,

∵BC为⊙OD 的直径,
∴CE⊥AB
又∵AC=BC,
∴AE=BE;
(2)连接OE,
∵点O、E分别是BC、AB的中点,
∴OE∥AC,
∵EG⊥AC,
∴OE⊥EF
∴FE是⊙O的切线;
(3)∵BC=2OE=6,
∴OE=3
∵FE=4,
∴OF=5
∴CF=2
∵OE∥AC,
∴△FCG∽△FEO
∴


又∵AC=BC=6,
∴
 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
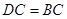 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 上,当
上,当 ∽
∽ 的长度.
的长度. 


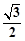


 上一点,求tan∠ADC的值.
上一点,求tan∠ADC的值. 的弦,半径OA=2,
的弦,半径OA=2, ,则弦AB的长为( )
,则弦AB的长为( )



 是
是 的弦,
的弦, 为半径
为半径 的中点,过
的中点,过 交弦
交弦 ,交
,交 ,且
,且 .
.
 是
是 、
、 ,求
,求 的度数;
的度数;