题目内容
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE= .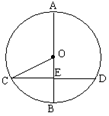


试题分析:先根据垂径定理及勾股定理求得OE的长,再根据锐角三角函数的定义求解即可.
∵CD⊥AB,CD=8
∴CE=4
∵直径AB=10
∴OC=5
∴

∴sin∠OCE=

 .
.点评:垂径定理与勾股定理的结合使用是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
题目内容




 .
.
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案