题目内容
在直角三角形ABC中，∠ACB=90°，AC=6，BC=8，O为AB上一点，OA=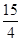
，以O为圆心，OA为半径作圆．
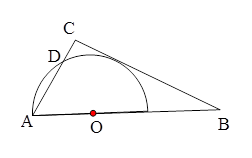
（1）试判断⊙O与BC的位置关系，并说明理由；
（2）若⊙O与AC交于另一点D，求CD的长．
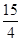，以O为圆心，OA为半径作圆．（1）试判断⊙O与BC的位置关系，并说明理由；
（2）若⊙O与AC交于另一点D，求CD的长．
相切；1.5
试题分析：(1)过点O作OE⊥BC 1分
∵∠ACB=90°,
∴△BOE∽△BAC 2分
∴
∴
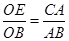
∴OE=
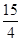4分∵OE⊥BC
∴⊙O与BC相切 5分
（2）过点O作OF⊥AC 6分
△AOF∽△ABC求得AF=
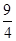8分由OF⊥AC，得AD=
9分∴CD=
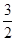10分点评：解答本题的的关键是熟练掌握有两组角对应相等的两个三角形相似；两组边对应成比例且夹角相等的三角形相似.
练习册系列答案
相关题目
是Rt
ABC的外接圆，
ABC=90
，点P是
，BC=2，求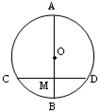
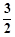
的弦，半径OA=2，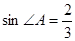
，则弦AB的长为( )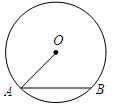
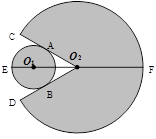
和弦AC的长.（弧长计算结果保留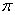
）