Question

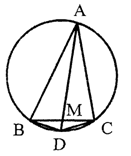
如图，在⊙O中，弦CD垂直于直径AB于点F，OF=3，CD=8，M是OC的中点，AM的延长线交⊙O于点E，DE与BC交于点N，（1）求AB的长；（2）求证：BN=CN.

Answer 1

（1）10 （2）证明C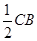N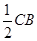=，所以CN=BN

试题分析：（1）AB是⊙O直径，AB⊥CD，CD=8
∴ CF=4                             
在Rt△OCF中，根据勾股定理，得
OC²=OF²+CF²                                  
=3²+4²
=25
∴OC=5                                      
∴AB=2OC=2×5=10                    
（2）连结AC，BD

∵弦CD垂直于直径AB，
∴BC=BD．
∴∠BCD=∠BDC   
∵OA=OC，                                                          
∴∠OCA=∠OAC．                                                                    
∵∠BDC=∠OAC，                                                                    
∴∠BCD=∠OCA．                                                                        
∴△BCD∽△OCA                                                                          
∴                                                                       
在△CDN和△CAM中，                                                                    
∵∠DCN=∠ACM，∠CDN=∠CAM，                                                       
∴△CDN∽△CAM                                                                          
∴
∴  
∴
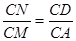
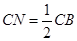
即BN=CN．  
点评：本题考查勾股定理，相似三角形，解答本题的关键是掌握勾股定理的内容，熟悉相似三角形的判定方法