题目内容
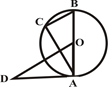
如图1,△ABC内接于半径为4cm的⊙O,AB为直径, 长为
长为 .
.

(1)计算∠ABC的度数;
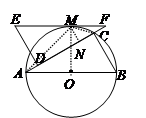
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;

(3)设图2中以A、C、M为顶点的三角形面积为S,求出S的值.
 长为
长为 .
.
(1)计算∠ABC的度数;
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过
 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;
(3)设图2中以A、C、M为顶点的三角形面积为S,求出S的值.
(1)60°;(2)连结OM,过点F作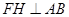 于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到
于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到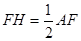 ,由点M为
,由点M为 的中点可得OM⊥AB且OM =
的中点可得OM⊥AB且OM =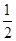 AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)
AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)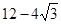
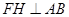 于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到
于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到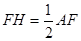 ,由点M为
,由点M为 的中点可得OM⊥AB且OM =
的中点可得OM⊥AB且OM =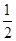 AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)
AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)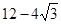
试题分析:(1)连结OC,先根据弧长公式求得∠BOC的度数,再结合圆的基本性质求解即可;
(2)连结OM,过点F作
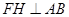 于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的性质可得到
于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的性质可得到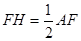 ,由点M为
,由点M为 的中点可得OM⊥AB且OM =
的中点可得OM⊥AB且OM =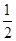 AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;
AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)连结AM、CM,过点M作MN⊥AC于点N,先根据含30°角的直角三角形的性质求得AC的长,在Rt△AMO中,根据勾股定理可求得AM的长,设MN=x,由∠MCN=
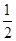
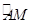 =45°可得MN=NC=x,在Rt△AMN中,根据勾股定理即可列方程求得x的值,最后根据三角形的面积公式求解即可.
=45°可得MN=NC=x,在Rt△AMN中,根据勾股定理即可列方程求得x的值,最后根据三角形的面积公式求解即可. (1)连结OC
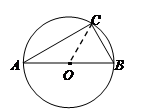
∵
 长为
长为 ,⊙O的半径为4cm
,⊙O的半径为4cm∴
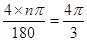 ,解得n=60,即∠BOC="60"
,解得n=60,即∠BOC="60" ∵OB=OC
∴∠ABC=∠OBC=
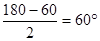 ;
;(2)连结OM,过点F作
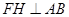 于H
于H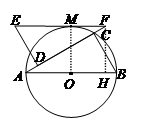
∵AB为直径
∴∠ACB=90°
∴∠A=180-90-60=30°
∴在Rt△FAH中,
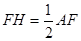
∵点M为
 的中点
的中点 ∴OM⊥AB且OM=
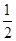 AB
AB∵△ABC与△FED全等
∴∠A=∠EFD=30°
∴EF∥AB,OM=FH=
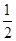 AB
AB∴AF=AB;
(3)连结AM、CM,过点M作MN⊥AC于点N
在Rt△ABC中,AB=8,∠A=30°
∴AC=4
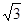
在Rt△AMO中,
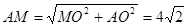
设MN="x" ,
∵∠MCN=
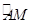 =45°
=45° ∴MN=NC=x
在Rt△AMN中,
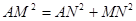
即
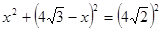
解得
 ,
,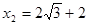 (舍去)
(舍去)∴
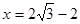
∴
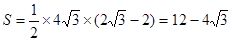 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,求AD的长.
,求AD的长.
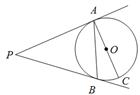
 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是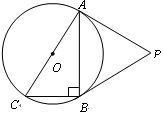
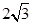 ,BC=2,求
,BC=2,求
 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
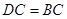 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出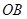 上,当
上,当 ∽
∽ 的长度.
的长度.