题目内容
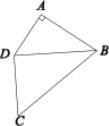
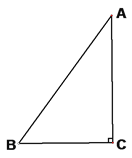
【题目】如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点 P 是线段 BC 上一动点(不与点 B,C 重合),若△APD 是等腰三角形,则 CP 的长是_______________.
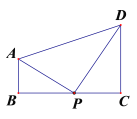
【答案】1或![]()
【解析】
过A作AM⊥CD于M,根据勾股定理求出AD,分为三种情况:AD=DP或AD=AP或AP=DP,根据勾股定理求出CP,再逐个判断即可.
如图:
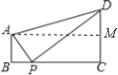
过A作AM⊥CD于M,
∵AB⊥BC,DC⊥BC,
∴∠AMD=90,∠B=∠C=∠AMC=90,
∴四边形ABCM是矩形,
∴CM=AB=1,AM=BC=3,
∴DM=21=1,
由勾股定理得:AD=![]() ,
,
∵△APD是等腰三角形,
∴分为三种情况:
①AP=DP,设CP=x,则BP=3x,
在Rt△ABP和Rt△DCP中,由勾股定理得:AB2+BP2=CP2+DC2,
即12+(3x)2=x2+22,
解得:x=1,
CP=1;
②AD=DP=![]() ,
,
CP= ![]() =
=![]() ;
;
③AD=AP=![]() ,
,
BP= ![]() ==3,
==3,
CP=33=0,此时P和C重合,不符合题意舍去;
故答案为:1或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目