题目内容
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
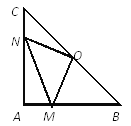
【答案】(1)OA=OB=OC. (2)△OMN为等腰直角三角形.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半,直接得出OA=OB=OC;
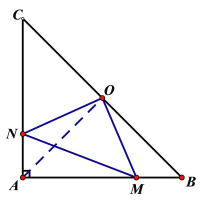
(2)连接OA,证△ANO≌△BMO,即可得出ON=OM,∠MON=90°,从而△OMN是等腰直角三角形.
(1)![]() .
.
(2)![]() .
.
证明:![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()

![]() ≌
≌![]() .
.
![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
故答案为:(1)OA=OC=OB (2)OMN为等腰直角三角形.

练习册系列答案
相关题目