题目内容
【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交X轴于B点,A(0,6),B(6,0).点D是线段BO上一点,BN⊥AD交AD的延长线于点N.
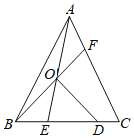
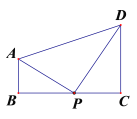
(1)如图,若OM∥BN交AD于点M.点O作0G⊥BN,交BN的延长线于点G,求证:AM=BG

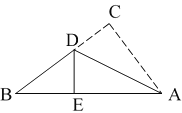
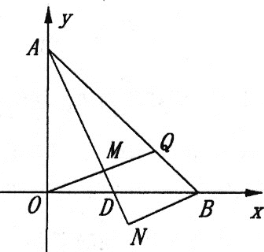
(2)如图,若∠ADO=67.5°,OM∥BN交AD于点M,交AB于点Q,求![]() 的值.
的值.
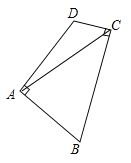
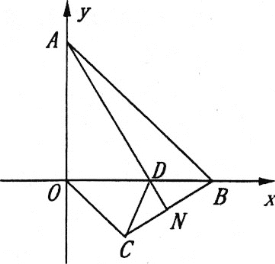
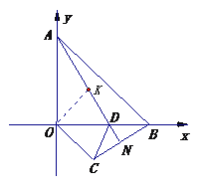
(3)如图,若OC∥AB交BN的延长线于点C.请证明:∠CDN+2∠BDN=180°.
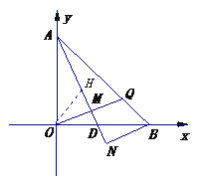
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)欲证明AM=BG,只要证明△AOM≌△BOG即可;
(2)在AD上截取AH=OQ,连接OH,先证明△AOH≌△△OBQ,推出∠AOH=∠OBQ=45°,推出HD=2MD.
(3)如图,作OE平分∠AOB交AD于K.只要证明△AOK≌△OBC,推出OK=OC,再证明△ODK≌△ODC,推出∠ODK=∠ODC,由∠ODK=∠BDN,可得∠ODC=∠BDN,由此即可解决问题.
(1) 在△AOM和△BOG中
∴△AOM≌△△BOG
∴AM=BG.
② 在AD上截取AH=OQ,连接OH,
∵∠ADO=67.5°∴∠OAD=∠BOQ=22.5°
易证∴△AOH≌△△OBQ
∴∠AOH=∠OBQ=45°
∴∠HOM=90°-45°-22.5°=22.5°=∠BOQ
有三线合一性质得HD=2MD
∴![]() =
=![]() =
=![]() =
=![]()
(3)作∠AOD的角平分线交AD于K
∵0C∥AB ∴∠ABO=∠BOC=∠AOK=∠BOK=450
 在△AOK和△BOC中
在△AOK和△BOC中
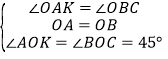
∴△AOK≌△△BOC
∴OK=OC
在△KOD和△DOC中
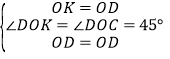
∴△KOD≌△△DOC
∴∠ODC=∠ODK=∠BDN
∴∠CDN+2∠BDN=180°.

练习册系列答案
相关题目