Question

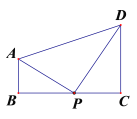
【题目】己知：在△ABC中，∠CAB＝2α，且0°＜α＜30°，AP平分∠CAB．

（1）如图，若α＝21°，∠ABC＝32°，且AP交BC于点P，试探究线段AB、AC与PB之间的数量关系，并对你的结论加以证明；

（2）如图，若∠ABC＝60°－α，点P在△ABC的内部，且使∠CBP＝30°，直接写出∠APC的度数________（用含α的代数式表示）．

Answer 1

【答案】（1）（1）AB-AC=PB，证明见解析；（2）120°+α.

【解析】

（1）在AB上截取AD，使AD=AC．连PD，证明△ACP≌△ADP，根据全等三角形的性质、三角形内角和定理证明PB=DB，证明结论；
（2）延长AC至M，使AM=AB，连接PM，BM，证明△AMP≌△ABP，根据等边三角形的性质、三角形内角和定理证明．

（1）AB-AC=PB，

在AB上截取AD，使AD=AC．连PD，

∵AP平分∠CAB，

∴∠CAP=∠BAP，

在△ACP和△ADP中，

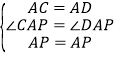
∴△ACP≌△ADP（SAS），

∴∠C=∠ADP．

∵△ABC中，∠CAB=42°，∠ABC=32°，

∴∠C=180°-∠CAB-∠ABC=180°-42°-32°=106°．

∴∠ADP=106°．

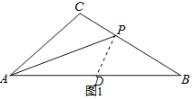
∴∠BDP=180°-∠ADP=180°-106°=74°，

∠BPD=∠ADP-∠ABC=106°-32°=74°．

∴∠BDP=∠BPD．

∴PB=DB，

∴AB-AC=AB-AD=DB=PB；

(2)如图2，延长AC到M使AM=AB, 120°+α.