题目内容
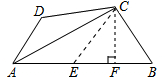
如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AB=21,AD=9.求AC的长.


∵AC平分∠BAD,
∴把△ADC沿AC翻折得△AEC,
∴AE=AD=9,CE=CD=10=BC.
作CF⊥AB于点F.
∴EF=FB=
BE=
(AB-AE)=6.
在Rt△BFC(或Rt△EFC)中,由勾股定理得CF=8.
在Rt△AFC中,由勾股定理得AC=17.
∴AC的长为17.
∴把△ADC沿AC翻折得△AEC,
∴AE=AD=9,CE=CD=10=BC.
作CF⊥AB于点F.
∴EF=FB=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BFC(或Rt△EFC)中,由勾股定理得CF=8.
在Rt△AFC中,由勾股定理得AC=17.
∴AC的长为17.


练习册系列答案
相关题目







