题目内容
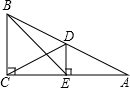
已知：如图，在△ABC中，AD平分∠BAC，CD⊥AD于点D，∠DCB=∠B，若AC=10，AD=6，求AB的长．
如图，延长CD交AB于点E．
∵AD平分∠BAC，
∴∠1=∠2．
∵CD⊥AD，
∴∠ADE=∠ADC=90°．
∵在△ADE与△ADC中，
，
∴△ADE≌△ADC（ASA）．
∴AE=AC=10，DE=DC．
∵∠DCB=∠B，
∴BE=CE=2DC．
∵在Rt△ACD中，AC=10，AD=6，
∴DC=
=
=8．
∴BE=CE=2DC=16．
∴AB=AE+BE=10+16=26．
∵AD平分∠BAC，
∴∠1=∠2．
∵CD⊥AD，
∴∠ADE=∠ADC=90°．
∵在△ADE与△ADC中，
|
∴△ADE≌△ADC（ASA）．
∴AE=AC=10，DE=DC．
∵∠DCB=∠B，
∴BE=CE=2DC．
∵在Rt△ACD中，AC=10，AD=6，
∴DC=
| AC2-CD2 |
| 102-62 |
∴BE=CE=2DC=16．
∴AB=AE+BE=10+16=26．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
