题目内容
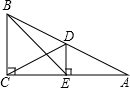
在Rt△ABC中,∠B=90°,B(0,0),A(0,4),C(4
,0).点D从点C出发沿CA方向以每秒2个单位的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)当t为何值时,线段DE长为
;
(2)当线段EF与以点B为圆心,半径为1的⊙B有两个公共交点时,求t的取值范围.

| 3 |
(1)当t为何值时,线段DE长为
| 39 |
(2)当线段EF与以点B为圆心,半径为1的⊙B有两个公共交点时,求t的取值范围.

(1)在Rt△ABC中,∠B=90°,B(0,0),A(0,4),C(4
,0),
∴tanC=OA:OC=
,
∴∠C=30°.
在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t,CF=
t,
∴OF=4
-
t,
∴D(4
-
t,t).
又∵AE=t,
∴OE=4-t.
∴E(0,4-t).
当线段DE长为
时,有(4
-
t)2+(t-4+t)2=39,
解得t1=
,t2=5(不合题意,舍去).
故t1=
时,线段DE长为
;
(2) ∵⊙B的半径为1,
∵⊙B的半径为1,
∴当点O到EF的距离小于1时,直线EF与⊙B相交.
而点O到EF的距离即为直角△EOF斜边EF上的高的长度,设直角△EOF斜边EF上的高为h.
∵AE∥DF,AE=DF=t,
∴四边形AEFD是平行四边形,
∴∠EFO=∠C=30°,
则h=OF•sin∠EFO=
OF=
,
∴
<1,
解得t>
.
又∵点D从点C出发沿CA方向运动,同时点E从点A出发沿AB方向运动,DF⊥BC于点F,
∴AE<4
故t的取值范围为:
<t<4.
| 3 |
∴tanC=OA:OC=
| ||
| 3 |
∴∠C=30°.
在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t,CF=
| 3 |
∴OF=4
| 3 |
| 3 |
∴D(4
| 3 |
| 3 |
又∵AE=t,
∴OE=4-t.
∴E(0,4-t).
当线段DE长为
| 39 |
| 3 |
| 3 |
解得t1=
| 5 |
| 7 |
故t1=
| 5 |
| 7 |
| 39 |
(2)
 ∵⊙B的半径为1,
∵⊙B的半径为1,∴当点O到EF的距离小于1时,直线EF与⊙B相交.
而点O到EF的距离即为直角△EOF斜边EF上的高的长度,设直角△EOF斜边EF上的高为h.
∵AE∥DF,AE=DF=t,
∴四边形AEFD是平行四边形,
∴∠EFO=∠C=30°,
则h=OF•sin∠EFO=
| 1 |
| 2 |
4
| ||||
| 2 |
∴
4
| ||||
| 2 |
解得t>
12-2
| ||
| 3 |
又∵点D从点C出发沿CA方向运动,同时点E从点A出发沿AB方向运动,DF⊥BC于点F,
∴AE<4
故t的取值范围为:
12-2
| ||
| 3 |

练习册系列答案
相关题目