��Ŀ����
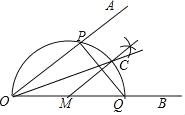
����Ŀ����֪��ADB����ͼ��
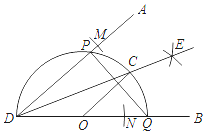
����1���Ե�DΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�DA��DB�ڵ�M��N���ٷֱ��Ե�M��NΪԲ�ģ�����![]() MN��Ϊ�뾶�������ڵ�E��������DE��
MN��Ϊ�뾶�������ڵ�E��������DE��
����2����DB����ȡһ��O���Ե�OΪԲ�ģ�OD��Ϊ�뾶����Բ���ֱ�DA��DB��DE�ڵ�P��Q��C��
����3������PQ��OC��
�������жϣ���![]() ����OC��DA����DP=PQ����OC��ֱƽ��PQ��������ȷ�Ľ����У�������
����OC��DA����DP=PQ����OC��ֱƽ��PQ��������ȷ�Ľ����У�������
A. �٢ۢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
���𰸡�B
��������
��DQΪֱ���ɵó�DA��PQ�����OC��PQ�ɵó�DA��OC����������ȷ������ͼ��֪��CDQ=��PDC�������ɵó���PC=��CQ ��OCƽ����AOB�������٢���ȷ������AOB�Ķ���δ֪�����ܵó�DP=PQ�����������������ϼ��ɵó����ۣ�
�⣺��DQΪֱ����
���DPQ=90�㣬DA��PQ��
��OC��PQ��
��DA��OC����������ȷ��
����ͼ��֪����CDQ=��PDC��
����PC=��CQ��OCƽ����AOB�������٢���ȷ��
�ߡ�ADB�Ķ���δ֪����PDQ����PQD���࣬
���PDQ��һ��������PQD��
��DP��һ������PQ������������
������������ȷ�Ľ������٢ڢܣ�
��ѡ��B��

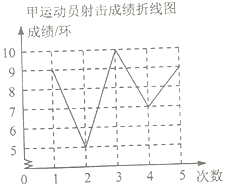
����Ŀ����16��ʡ�˻�������¡�ؾ��У��ƶ������и�У����������ݱ�Ŀ�չ����ijУ����ӵ�һ��ѵ���У��ף��������˶�Աǰ5����ƽ���ɼ���ͬ�����������˵ijɼ����Ƴ������в�������ͳ��ͼ��.
���˶�Ա�ɼ�ͳ�Ʊ�(��λ����)
��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
8 | 10 | 8 | 6 |
|
(1)���˶�Աǰ5������ɼ��������� ������λ���� ����
(2)�����˶�Ա��5�εijɼ���
(3)�������ѡ��һ���ɼ��ȶ����˶�Ա�μ�ȫ����ѧ������������ΪӦѡ˭ȥ����˵������.
����Ŀ��ij�꼶380��ʦ�����Σ��ƻ�����7���ͳ������мס��������ͺſͳ������ǵ��ؿ�������������
���ֿͳ� | ���ֿͳ� | |
�ؿ�������/���� | 60 | 45 |
���Ԫ/���� | 550 | 450 |
��1�������ü��ֿͳ�x������ܷ���ΪyԪ�����y��Ԫ����x������֮��ĺ�������ʽ��
��2�������ֿͳ��ж�����ʱ���ܱ������е�ʦ���ܲμ���������������٣����ٷ����Ƕ���Ԫ��