题目内容
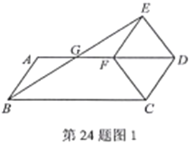
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)

【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)BG=EG,根据已知条件易证△BAG≌△EFG,根据全等三角形的对应边相等即可得结论;(2)①方法一:过点G作GM∥BH,交DH于点M,证明ΔGME∽ΔBHE,即可得![]() ,再证明
,再证明![]() 是等边三角形,可得
是等边三角形,可得 ![]() ,由此可得
,由此可得![]() ;方法二:延长
;方法二:延长![]() ,
,![]() 交于点
交于点![]() ,证明ΔHBM为等边三角形,再证明
,证明ΔHBM为等边三角形,再证明![]() ∽
∽![]() ,即可得结论;②如图3,连接EC交DF于O根据三角函数定义得cosα=
,即可得结论;②如图3,连接EC交DF于O根据三角函数定义得cosα=![]() ,则OF=bcosα,DG=a+2bcosα,同理表示AH的长,代入
,则OF=bcosα,DG=a+2bcosα,同理表示AH的长,代入![]() 计算即可.
计算即可.
(1)![]() ,
,
理由如下:
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∥
∥![]() ,
,![]() .
.
∵四边形![]() 是菱形,
是菱形,
∴![]() ∥
∥![]() ,
,![]() .
.
∴![]() ∥
∥![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ≌
≌![]()
![]() .
.
∴![]() .
.
(2)方法1:过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,
,
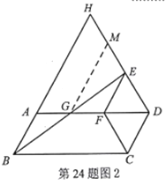
∴![]() .
.
∵![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() .
.
由(1)结论知![]() .
.
∴![]() .
.
∴![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∥
∥![]() .
.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() ,
,
即![]() .
.
∴![]() 是等边三角形。
是等边三角形。
∴![]() .
.
∴![]() .
.
方法2:延长![]() ,
,![]() 交于点
交于点![]() ,
,
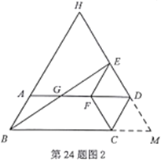
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∵四边形![]() 为平形四边形,
为平形四边形,
∴![]() ,
,![]() ∥
∥![]() .
.
∴![]() .
.
![]() ,
,
即![]() .
.
∴![]() 为等边三角形.
为等边三角形.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ∽
∽![]() ,
,
∴![]() .
.
由(1)结论知![]()
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(3)![]() . 如图3,连接EC交DF于O,
. 如图3,连接EC交DF于O,
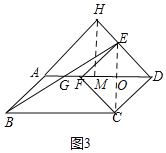
∵四边形CFED是菱形,
∴EC⊥AD,FD=2FO,
设FG=a,AB=b,则FG=a,EF=ED=CD=b,
Rt△EFO中,cosα=![]() ,
,
∴OF=bcosα,
∴DG=a+2bcosα,
过H作HM⊥AD于M,
∵∠ADC=∠HAD=∠ADH=α,
∴AH=HD,
∴AM=![]() AD=
AD=![]() (2a+2bcosα)=a+bcosα,
(2a+2bcosα)=a+bcosα,
Rt△AHM中,cosα=![]() ,
,
∴AH=![]() ,
,
∴![]() =
=![]() =cosα.
=cosα.

 发散思维新课堂系列答案
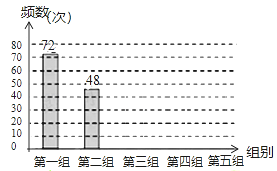
发散思维新课堂系列答案【题目】某网络约车公司近期推出了”520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图(如图).
组别 | 单次营运里程“x“(公里) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据统计表、图提供的信息,解答下面的问题:
(1)①表中a= ;②样本中“单次营运里程”不超过15公里的频率为 ;③请把频数分布直方图补充完整;
(2)请估计该公司这5000个“单次营运里程”超过20公里的次数;
(3)为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机(3男1女)成立了“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率.