��Ŀ����
����Ŀ�����������壩
���ı��ε�һ���Խ����ܽ��ı��ηָ���������Ƶ�ֱ�������Σ���ô���ǽ������ı��ν�������Ծ�ı��Ρ��������Խ��߽�������Ծ�ߡ���
��������
��1�����⡰���Ǿ��ζ�����Ծ�ı��Ρ���ʲô���⣨���桱�١�����
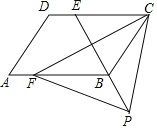
��2���ı���ABCDΪ����Ծ�ı��Ρ����ҶԽ���ACΪ����Ծ�ߡ�������AC��CB����B=30�㣬AB=4![]() �����ı���ABCD���ܳ���
�����ı���ABCD���ܳ���
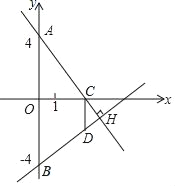
��ʵ��Ӧ�ã���֪������y=ax2+m��a��0����x�ύ��B����2��0����C���㣬��ֱ��y=2x+b����A��B���㣮
��3��ֱ��д��C�����꣬����������ߵĽ���ʽ��
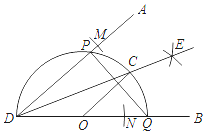
��4�����߶�AB����һ����P��������BC����һ����Q��P��Q����ֱ���![]() ����λ/�룬5����λ/����ٶ�ͬʱ��B��������BA��BC�����˶������˶�ʱ��Ϊt��������һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶����ڵ�һ�������������Ƿ���ڵ�M��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ��������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
����λ/�룬5����λ/����ٶ�ͬʱ��B��������BA��BC�����˶������˶�ʱ��Ϊt��������һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶����ڵ�һ�������������Ƿ���ڵ�M��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ��������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
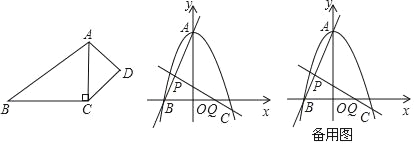
���𰸡�����������1�����Ǿ��ζ�����Ծ�ı���������������2���ı���ABCD���ܳ�Ϊ12+4![]() ��12+8
��12+8![]() ��9+5
��9+5![]() ����ʵ��Ӧ�á���3��
����ʵ��Ӧ�á���3��![]() ��
��![]() ����4��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ���ʱ��t��ֵΪ��t=
����4��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ���ʱ��t��ֵΪ��t=![]() ��t=
��t=![]() ��t=
��t=![]() ��t=
��t=![]() .
.
��������
�����������1���ɶ����ֱ�ӵã�
��2���������DAC=90������ADC=90������������ۣ������ı���ABCD���ܳ���
ʵ��Ӧ������3�����ݵ�B����C���ڶԳ���Գƣ������C���꣬�ô���ϵ�������������߽���ʽ��
��4���������֤��ABO�ס�BPQ����֤PQ��AB���ı���BQMP����PQΪ����Ծ����������Ծ�ı��������ɵ���BPQ�ס�PQM������PQM=90������PMQ=90������������ۣ�����t��ֵ��
��������1�������εĶԽ������ֵ�����������ȫ��
�����Ǿ��ζ�����Ծ�ı�����������
�ʴ�Ϊ�����Ǿ��ζ�����Ծ�ı����������⣮
��2����AC��BC����B=30�㣬AB=4![]()
��AC=2![]() ��BC=6
��BC=6
����CAD=90��ʱ��
��ͼ1��
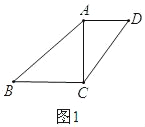
���ı���ABCDΪ����Ծ�ı��Ρ�
���ABC�ס�CAD
��![]() ��
��![]()
��AD=2��CD=4��AD=6��CD=4![]()
���ı���ABCD���ܳ�=AB+BC+CD+AD=2+4+4![]() +6=12+4
+6=12+4![]()
���ı���ABCD���ܳ�=AB+BC+CD+AD=6+4![]() +6+4
+6+4![]() =12+8
=12+8![]()
����ADC=90��
��ͼ2��

���ı���ABCDΪ����Ծ�ı��Ρ�
���ABC�ס�CAD
��![]() ��
��![]()
��AD=![]() ��CD=3��AD=3��CD=
��CD=3��AD=3��CD=![]()
���ı���ABCD���ܳ�=AB+BC+CD+AD=6+4![]() +3+
+3+![]() =9+5
=9+5![]()
���ı���ABCD���ܳ�=AB+BC+CD+AD=6+4![]() +3+
+3+![]() =9+5
=9+5![]()
�����������ı���ABCD���ܳ�Ϊ12+4![]() ��12+8
��12+8![]() ��9+5
��9+5![]()
ʵ��Ӧ�ã���3����������y=ax2+m��a��0����x�ύ��B����2��0����C����
����������Ϊ��0��m�����Գ���Ϊy�ᣬ��B����C���ڶԳ���Գ�
����C��2��0��
��������y=ax2+m��ֱ��y=2x+b���ڵ�A����B
��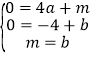
��m=b=4��a=��1
�������߽���ʽy=��x2+4
��P��Q����ֱ���![]() ����λ/�룬5����λ/����ٶ�
����λ/�룬5����λ/����ٶ�
�����˶�ʱ��Ϊt
��BP=![]() t��BQ=5t
t��BQ=5t
����A��0��4������B����2��0��
��OA=4��OB=2
��AB=2![]()
��![]() ����ABO=��PBQ
����ABO=��PBQ
���ABO�ס�PBQ
���AOB=��BPQ=90��
���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı���
���BPQ�ס�PQM
���PQM��ֱ��������
������PQM=90��ʱ����BP��QM�Ƕ�Ӧ�ߣ���PD��BC����ME��BC��
��ͼ3
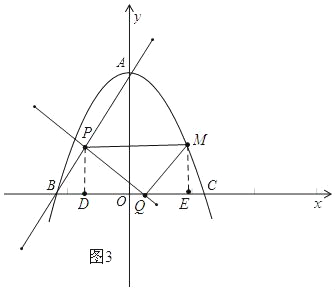
�ߡ�BPQ�ס�PQM
��![]()
��BP=QM��PM=BQ
���ı���BPMQ��ƽ���ı���
��BP��QM
���PBD=��MQE
��BP=MQ����PBD=��MQE����PDB=��MEQ
���BPD�ա�MQE
��PD=ME��BD=QE
��PD��AO
��![]()
��![]()
��BD=t��PD=2
��QE=t��ME=2t
��OE=BQ+QE��BO=6t��2
��M��6t��2��2t�����ҵ�M����������
��2t=����6t��2��2+4
��t=![]()
������PQM=90��ʱ����BP��PQ�Ƕ�Ӧ�ߣ���PD��BC����ME��BC��
��ͼ4
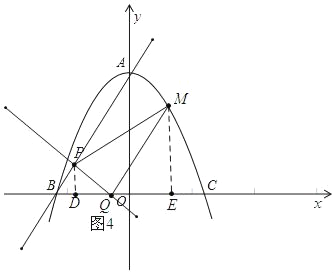
�ߡ�BPD�ס�MQE
��![]()
��![]()
��QM=4![]() t
t
�ߡ�BQP+��PBQ=90�㣬��BQP+��MQE=90��
���PBQ=��MQE����BPQ=��MEQ=90��
���BPQ�ס�MEQ
��![]()
��ME=8t��QE=4t
��OE=BQ+QE��BO=9t��2
��M��9t��2��8t�����ҵ�M����������
��8t=����9t��2��2+4
��t=![]()
������PMQ=90�㣬BP��MQ�Ƕ�Ӧ�ߣ�����P��PD��BC
��ͼ5

�ߡ�BPQ�ס�MQP
���PQB=��MPQ
��PM��BC
��MQ��PM
��MQ��BC����PD��BC
��MQ��PD
���ı���PDQM��ƽ���ı�����PD��BC
���ı���PDQM�Ǿ���
��PD=MQ
��BD=t��PD=2t��BQ=5t
��QM=2t
��OQ=BQ��BO=5t��2
��M��5t��2��2t���ҵ�M����������
��2t=����5t��2��2+4
��t=![]()
������PMQ=90�㣬BP��MP�Ƕ�Ӧ�ߣ�����M��EF��BC������P��PD��BC���ӳ�DP��EF��F��
����Q��EQ��EF��F��
��ͼ6
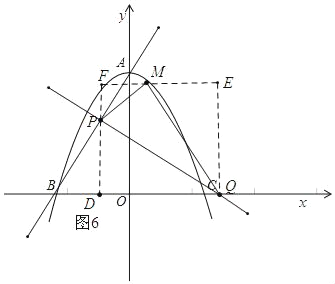
�ߡ�BPQ�ס�PMQ
���MQP=��BQP
����PD��BC��PM��MQ
��PD=PM=2t
��PD=PM��PQ=PQ
���PDQ�ա�PQM
��MQ=DQ=BQ��BD=5t��t=4t
��FE��BC��EQ��EF��DFBC
��DF��EF��EQ��BC
���ı���EFDQ�Ǿ���
��EF=DQ=4t
�ߡ�FMP+��FPM=90�㣬��EMQ+��FMP=90��
���FPM=��EMQ����E=��MFD=90��
���FMP�ס�MEQ
��![]()
��EQ=2FM
��Rt��MEQ��MQ2=EQ2+ME2
�ࣨ4t��2=��2FM��2+��4t��FM��2
��FM=![]() t
t
��EQ=![]() t
t
��M��![]() t��2��
t��2��![]() t�����ҵ�M����������
t�����ҵ�M����������
��![]() t=����
t=����![]() t��2��2+4
t��2��2+4
��t=![]()
����������ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ���ʱ��t��ֵΪ��t=![]() ��t=
��t=![]() ��t=
��t=![]() ��t=
��t=![]()

 �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�