题目内容
如图,E为□ABCD中DC边延长线上的一点,且CE=CD,连接AE,分别交BC、BD于点F、G.
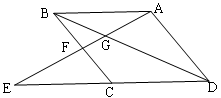
(1)求证:△AFB≌△EFC;
(2)若BDD=12厘米,求DG的长.

(1)求证:△AFB≌△EFC;
(2)若BDD=12厘米,求DG的长.
(1)先根据平行四边形的性质可得∠BAE=∠FEC,∠ABF=∠ECF,再结合CE=CD可得AB=CE,根据“ASA”,即可证得结论;(2)8
试题分析:(1)先根据平行四边形的性质可得∠BAE=∠FEC,∠ABF=∠ECF,再结合CE=CD可得AB=CE,根据“ASA”,即可证得结论;
(2)根据平行线分线段成比例的性质可得
 ,再结合BD的长即可求得结果.
,再结合BD的长即可求得结果.(1)在□ABCD中,AB//CD
∴∠BAE=∠FEC,∠ABF=∠ECF
∵CE=CD
∴AB=CE
∴△AFB≌△EFC(ASA);
(2)∵AB//CD
∴

∴

∵

∴
 厘米.
厘米.点评:解题的关键是熟练掌握平行四边形的对边平行且线段,平行线分线段成比例.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目





 cm2;
cm2; cm2;
cm2; cm2;
cm2; cm2.
cm2.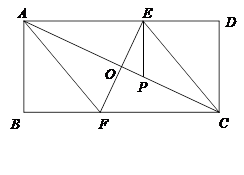
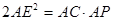 ,求证:CD∥PE.
,求证:CD∥PE.