题目内容
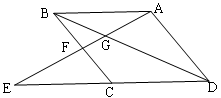
如图:在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是 

菱形
试题分析:连接AC、BD,因为△ADE和△BCE都是等边三角形,所以
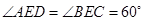 ,所以
,所以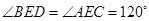 ,又
,又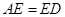 ,
,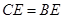 ,所以△AEC≌△EDB,所以
,所以△AEC≌△EDB,所以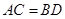 ,又P、Q、M、N为各边中点,所以
,又P、Q、M、N为各边中点,所以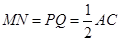 且MN∥AC∥PQ,同理,
且MN∥AC∥PQ,同理,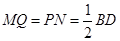 且MQ∥BD∥PN,即四边形MNPQ为平行四边形,且
且MQ∥BD∥PN,即四边形MNPQ为平行四边形,且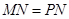 ,则平行四边形MNPQ为菱形
,则平行四边形MNPQ为菱形点评:本题关键在于利用三角形的全等,求出

练习册系列答案
相关题目
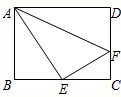
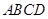 中,
中,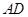 ∥
∥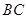 ,已知
,已知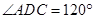 ,
,
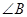 的度数;
的度数;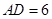 ,
,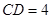 ,试求等腰梯形
,试求等腰梯形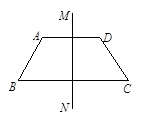
 中,
中, 是
是 边上的一点,
边上的一点,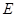 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.