题目内容
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
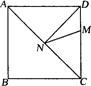
已知:如图,在矩形ABCD中,点E、F分别在边AD、BC上,EF垂直平分AC,垂足为O,联结AF、CE.
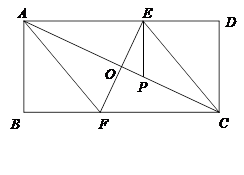
(1)求证:四边形AFCE是菱形;
(2)点P在线段AC上,满足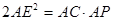 ,求证:CD∥PE.
,求证:CD∥PE.
已知:如图,在矩形ABCD中,点E、F分别在边AD、BC上,EF垂直平分AC,垂足为O,联结AF、CE.

(1)求证:四边形AFCE是菱形;
(2)点P在线段AC上,满足
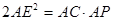 ,求证:CD∥PE.
,求证:CD∥PE.(1)四边形AFCE是菱形,(2)CD//PE.
试题分析:证明:(1)∵四边形ABCD矩形,∴AD∥BC,∴
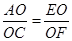 (2分)
(2分)∵EF平分AC,∴AO=OC,∴EO=OF (1分)
∴四边形AFCE是平行四边形 (1分)
∵EF⊥AC,∴四边形AFCE是菱形. (1分)
(2)∵EF垂直平分AC,∴AC=2AO,∠AOE=90° (1分)
∵
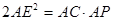 ,∴
,∴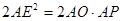 ,∴
,∴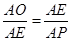 (1分)
(1分)∵∠EAP=∠OAE,∴△AOE∽△AEP (1分)
∴∠AEP=∠AOE=90° (1分)
又∵四边形ABCD是矩形,∴∠D=90° (1分)
∴∠AEP=∠D (1分)
∴CD∥PE (1分)
点评:熟练掌握以上几个特殊图形的概念及性质,结合已知不难求出结论,对概念性质的理解是解决本题的关键,利用相似三角形的性质,得到边与边,角与角的关系,本题属于中档题,有一定的难度。

练习册系列答案
相关题目
 中,
中,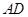 ∥
∥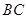 ,已知
,已知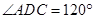 ,
,
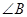 的度数;
的度数;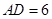 ,
,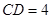 ,试求等腰梯形
,试求等腰梯形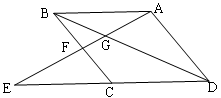
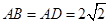 ,求四边形ABCD的面积.
,求四边形ABCD的面积.
 垂直平分
垂直平分 ,
, ㎝,
㎝, ㎝,则四边形
㎝,则四边形 的周长是 ㎝.
的周长是 ㎝.
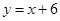 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.