题目内容
【题目】如图，一条东西走向的笔直公路，点A、B表示公路北侧间隔150米的两棵树所在的位置，点C表示电视塔所在的位置．小王在公路PQ南侧直线行走，当他到达点P的位置时，观察树A恰好挡住电视塔，即点P、A、C在一条直线上，当他继续走180米到达点Q的位置时，以同样方法观察电视塔，观察树B也恰好挡住电视塔．假设公路两侧AB∥PQ，且公路的宽为60米，求电视塔C到公路南侧PQ的距离．
【答案】电视塔C到公路南侧所在直线PQ的距离是360米．
【解析】
作CE⊥PQ交AB于D点，利用相似三角形对应边上的高的比等于相似比，即可求得电视塔到公路南侧所在直线的距离．
如图所示，作CE⊥PQ于E，交AB于D点，
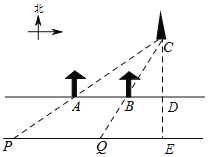
设CD为x，则CE=60+x，
∵AB∥PQ，
∴△ABC∽△PQC，
∴
=
，即
=
，
解得x=300，
∴x+60=360米，
答：电视塔C到公路南侧所在直线PQ的距离是360米．
练习册系列答案
相关题目
