题目内容
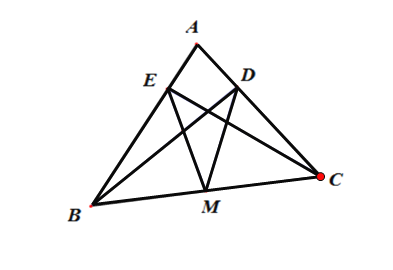
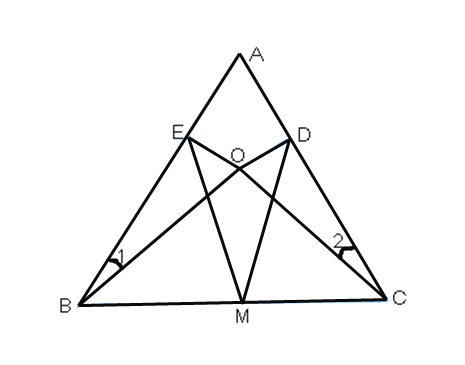
【题目】如图所示,⊙O半径为2,弦BD=2![]() ,A为弧BD的中点,E为弦AC的中点,且在BD上,求四边形ABCD的面积.
,A为弧BD的中点,E为弦AC的中点,且在BD上,求四边形ABCD的面积.

【答案】![]() .
.
【解析】
由A是弧BD的中点,根据垂径定理,可知OF⊥BD,且BF=DF=![]() ×BD×AF=
×BD×AF=![]() ,而E是AC中点,会出现等底同高的三角形,因而有S四边形=2S△ABD=2
,而E是AC中点,会出现等底同高的三角形,因而有S四边形=2S△ABD=2![]() .
.
连结OA交BD于点F,连接OB.

∵OA在直径上且点A是BD中点,
∴OA⊥BD, BF=DF=![]() .
.
在Rt△BOF中,由勾股定理得OF2=OB2-BF2,
OF=![]()
![]()
![]()
![]() =
=![]() .
.
∵点E 是AC中点,
∴AE=CE.
又∵△ADE和△CDE同高,
∴S△CDE=S△ADE,
同理S△CBE =S△ABE,
∴S△BCD =S△CDE +S△CBE =S△ADE +S△ABE =S△ABD =![]() ,
,
∴S四边形ABCD=S△ABD +S△BCD =2![]() .
.

练习册系列答案
相关题目
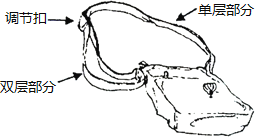
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小垣用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | ______ | … | ______ |
(2)根据小垣的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度.