题目内容
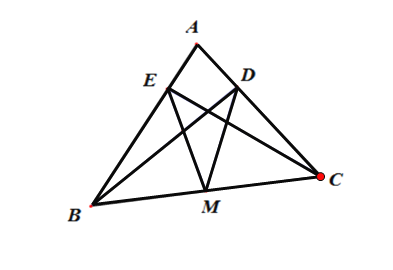
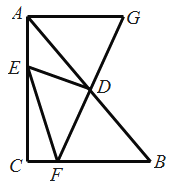
【题目】如图,在![]() 中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使
中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使![]() ,连接EF、AG,已知
,连接EF、AG,已知![]() ,
,![]() ,
,![]() .
.
(1)试说明![]() ;
;
(2)请你连接EG,设![]() ,
,![]() ,求y关于x的函数关系式;
,求y关于x的函数关系式;
(3)当![]() 是以BF为腰的等腰三角形时,直接写出AE的长,不必说明理由.
是以BF为腰的等腰三角形时,直接写出AE的长,不必说明理由.
【答案】(1)见解析;(2)![]() ;(3)AE的长度为
;(3)AE的长度为![]() 或
或![]()
【解析】
(1)由D是AB中点知AD=DB,结合DG=DF,∠ADG=∠BDF即可证得![]() ,从而可得结论;
,从而可得结论;
(2)连接EG.根据垂直平分线的判定定理即可证明EF=EG,由△ADG≌△BDF,推出∠GAB=∠B,推出∠EAG=90°,可得EF2=(8-x)2+y2,EG2=x2+(6-y)2,根据EF=EG,可得(8-x)2+y2=x2+(6-y)2,由此即可解决问题;
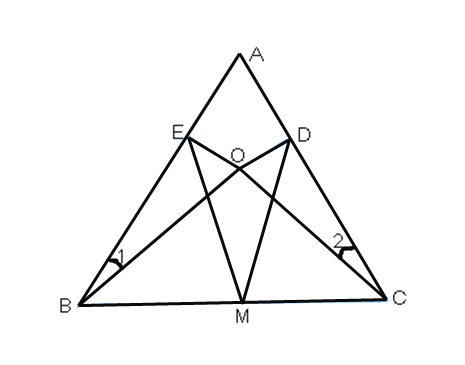
(3)如图2中,分两种情况讨论即可.①当BF=DB时.②当DF=FB时,连接DC,过点D作DH⊥BC于H,想办法求出y的值,再利用(2)的结论即可解决问题.
(1)∵D是AB中点,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
(2)如图,连接EG.
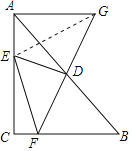
∵DG=FD,DF⊥DE,
∴EF=EG.
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,且
是直角三角形,且![]() ,
,
∴![]() ,
,
由(1)知![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)如图2中,
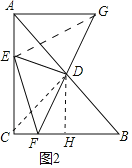
①当BF=DB时,6-y=5,
∴y=1,1=![]() ,
,
∴x=![]() ,即AE=
,即AE=![]() .
.
②当DF=FB时,连接DC,过点D作DH⊥BC于H,则DF=FB=6-y,
∵∠ACB=90°,D是AB中点,
∴DC=DB=5,
∵DH⊥BC,BC=6,
∴CH=BH=3,
∴FH=3-y,
∵DH⊥BC,由勾股定理可得DH=4,
在Rt△DHF中,(6-y)2=42+(3-y)2,
解得y=![]() ,
,
∴![]() =
=![]() ,
,
解得x=![]() ,即AE=
,即AE=![]() .
.
综上所述,AE的长度为![]() 或
或![]() .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小垣用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | ______ | … | ______ |
(2)根据小垣的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度.