题目内容
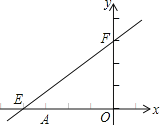
【题目】如图,正方形ABCD的顶点A、B在x轴上,顶点D在反比例函数y=![]() (k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )
(k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
设正方形ABCD的边长为a,A(x,0),则D(x,a),再由点D在反比例函数y=![]() 的图象上可知,k=xa,根据正方形的性质得出∠CAB的度数,根据对顶角相等可得出∠OAE的度数,进而判断出△OAE的形状,故可得出E点坐标,根据△ABE的面积为2即可得出k的值.
的图象上可知,k=xa,根据正方形的性质得出∠CAB的度数,根据对顶角相等可得出∠OAE的度数,进而判断出△OAE的形状,故可得出E点坐标,根据△ABE的面积为2即可得出k的值.
设正方形ABCD的边长为a,A(x,0),则D(x,a),
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴k=xa,
∵四边形ABCD是正方形,
∴∠CAB=45°,
∴∠OAE=∠CAB=45°,
∴△OAE是等腰直角三角形,
∴E(0,-x),
∴S△ABE=![]() ABOE=
ABOE=![]() ax=2,
ax=2,
∴ax=4,即k=4.
故选D.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目