题目内容
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.(参考数据:tan400=0.84, sin400=0.64, cos400= )
)
小题1:求钢缆CD的长度;(精确到0.1米)
小题2:若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?

 )
)小题1:求钢缆CD的长度;(精确到0.1米)
小题2:若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?

小题1:(1)在R t△BCD中,
 ,
,∴

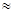 6.7,
6.7,小题2:在R t△BCD中, BC=5, ∴ BD=5 tan400=4.2.
过E作AB的垂线,垂足为F,在R t△AFE中,AE=1.6,
∠EAF=180O-120O=60O,AF=
 =0.8 ∴FB=AF+AD+BD=0.8+2+4.20=7米 答:钢缆CD的长度为6.7米,灯的顶端E距离地面7米.
=0.8 ∴FB=AF+AD+BD=0.8+2+4.20=7米 答:钢缆CD的长度为6.7米,灯的顶端E距离地面7米.析:(1)利用三角函数求得CD的长;
(2)过E作AB的垂线,垂足为F,根据三角函数求得BD、AF的长,则FB的长就是点E到地面的距离.
解答:解:(1)在Rt△BCD中,

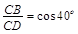 ,
,
∴ ≈6.7;
≈6.7;
(2)在Rt△BCD中,BC=5,∴BD=5tan40°=4.2.
过E作AB的垂线,垂足为F,
在Rt△AFE中,AE=1.6,∠EAF=180°-120°=60°,
AF=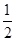 AE=0.8
AE=0.8
∴FB=AF+AD+BD=0.8+2+4.20=7米.
答:钢缆CD的长度为6.7米,灯的顶端E距离地面7米.
(2)过E作AB的垂线,垂足为F,根据三角函数求得BD、AF的长,则FB的长就是点E到地面的距离.
解答:解:(1)在Rt△BCD中,

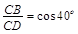 ,
,∴
 ≈6.7;
≈6.7;(2)在Rt△BCD中,BC=5,∴BD=5tan40°=4.2.
过E作AB的垂线,垂足为F,
在Rt△AFE中,AE=1.6,∠EAF=180°-120°=60°,
AF=
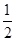 AE=0.8
AE=0.8∴FB=AF+AD+BD=0.8+2+4.20=7米.
答:钢缆CD的长度为6.7米,灯的顶端E距离地面7米.

练习册系列答案
相关题目
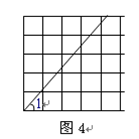
 ,OD=20.(1)求∠ABC的度数;(2)连接BE,求线段BE的长
,OD=20.(1)求∠ABC的度数;(2)连接BE,求线段BE的长
 ,求c及∠B.
,求c及∠B.


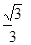 ,则边BC 的长为( ).
,则边BC 的长为( ).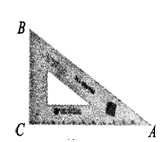
 cm
cm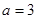 ,且
,且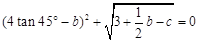 ,以a、b、c为边组成的三角形面积
,以a、b、c为边组成的三角形面积