题目内容
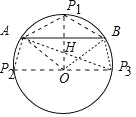
【题目】已知⊙O 的直径为 4,AB 是⊙O 的弦,∠AOB=120°,点 P 在⊙O 上,若点 P到直线 AB 的距离为 1,则∠PAB 的度数为_____.
【答案】15°或 30°或 105°
【解析】
作 OP1⊥AB 交⊙O 于 P1 交 AB 于 H,过点 O 作直线 P2P3∥AB 交⊙O 于 P2,P3.由垂径定理可得∠AOH=60°,进而可得∠OAH=30°,即可求出OH=1,进而可知P1,P2,P3 是满足条件的点,根据圆周角定理求出∠P1AB、∠P3AB、∠P2AB的度数即可.
如图作 OP1⊥AB 交⊙O 于 P1 交 AB 于 H,过点 O 作直线 P2P3∥AB 交⊙O 于 P2,P3.
∵∠AOB=120°,OA=OB,OH⊥AB,
∴∠AOH=![]() ∠AOB=60°,∠AHO=90°,
∠AOB=60°,∠AHO=90°,
∴∠OAH=30°,
∵⊙O 的直径为 4,
∴OH=![]() OA= 1,
OA= 1,
∴HP1=1,
∴直线 AB 与直线 P2P3 之间的结论距离为 1,
∴P1,P2,P3 是满足条件的点,
∴∠P1AB=![]() ∠BOP1=30°,∠P3AB=
∠BOP1=30°,∠P3AB=![]() ∠BOP3=15°,
∠BOP3=15°,
∵P2P3是⊙O的直径,
∴∠P2AP3=90°,
∴∠P2AB=∠P2AP3+∠P3AB=90°+15°=105°,
故答案为:15°或 30°或 105°.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目