题目内容
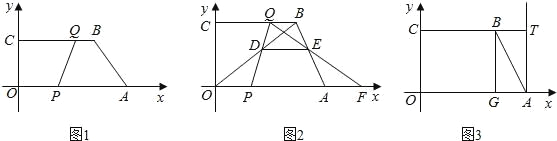
【题目】四边形 OABC 在图 1 中的直角坐标系中,且OC在 y 轴上,OA∥BC,A、B两点的坐标分别为 A(18,0),B(12,8),动点 P、Q分别从 O、B两点出发,点 P以每秒2个单位的速度沿 OA 向终点 A 运动,点 Q 以每秒1个单位的速度沿BC向 C运动,当点 P停止运动时,点 Q 同时停止运动.动点 P、Q 运动时间为 t(单位:秒).
(1)当 t 为何值时,四边形 PABQ 是平行四边形,请写出推理过程;
(2)如图 2,线段 OB、PQ 相交于点 D,过点 D 作 DE∥OA,交 AB 于点 E,射线 QE 交 x 轴于点 F,PF=AO.当 t 为何值时,△PQF 是等腰三角形?请写出推理过程;
(3)如图 3,过 B 作 BG⊥OA 于点 G,过点 A 作 AT⊥x 轴于点 A,延长 CB 交 AT于点 T.将点 G 折叠,折痕交边 AG、BG 于点 M、N,使得点 G 折叠后落在AT 边上的点为 G′,求 AG′的最大值和最小值.
【答案】(1)当 t 为 6 时,四边形 PABQ 是平行四边形;(2)当 t=1 或 t=![]() 时,△PQF 是等腰三角形;(3)AG′的最大值与最小值分别是 6,8﹣2
时,△PQF 是等腰三角形;(3)AG′的最大值与最小值分别是 6,8﹣2![]() .
.
【解析】
(1)由梯形的性质得出当 PA=BQ 时,四边形 PABQ 是平行四边形,BQ=t,
OP=2t,得出方程,解方程即可;
![]() 过 Q作 QH⊥OF 于 H,①当 FP=FQ 时,求出 CQ=OH=12﹣t,PH=12﹣3t, 得出 FH=3t+6,由勾股定理得出方程,解方程即可;
过 Q作 QH⊥OF 于 H,①当 FP=FQ 时,求出 CQ=OH=12﹣t,PH=12﹣3t, 得出 FH=3t+6,由勾股定理得出方程,解方程即可;
②当 PF=PQ 时,PQ=P F=18,在 Rt△PQH 中,由勾股定理得出方程,解方程即可;
③当 PQ=FQ 时,PH=FH,得出方程 12﹣3t=6+3t,解方程即可;
![]() 当折痕经过点 A 时,AG=AG′=6,此时 AG′为最大值;当折痕经过点 B,另一点在 AG 上时 AG′最小,此时,BG=BG′=8,在 Rt△BG′T 中,由勾股定理求出TG′,得出
当折痕经过点 A 时,AG=AG′=6,此时 AG′为最大值;当折痕经过点 B,另一点在 AG 上时 AG′最小,此时,BG=BG′=8,在 Rt△BG′T 中,由勾股定理求出TG′,得出 ![]() 即可.
即可.
(1)∵OA∥BC,
∴PA∥BQ,
当 PA=BQ 时,四边形 PABQ 是平行四边形,BQ=t,OP=2t,
∵A(18,0),
∴PA=18﹣2t,
∴t=18﹣2t, 解得:t=6,
∴当 t 为 6 时,四边形 PABQ 是平行四边形;
(2)过 Q 作 QH⊥OF 于 H,如图 1 所示:
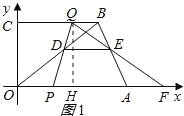
分三种情况:
①当 FP=FQ 时,
∵PF=AO=18,
∴FQ=18,BQ=t,
∴CQ=OH=12﹣t,
∴PH=12﹣3t,
∴FH=3t+6,
在 Rt△QHF 中,由勾股定理得:QH2+FH2=FQ2,
∴82+(3t+6)2=182,
解得:t1=![]() ,t2=
,t2=![]() (不合题意舍去);
(不合题意舍去);
②当 PF=PQ 时,PQ=PF=18,
在 Rt△PQH 中,由勾股定理得:PQ2=PH2+QH2,
∴(12﹣3t)2+82=182,
解得:t1=![]() (不合题意舍去),t2=
(不合题意舍去),t2=![]() (不合题意舍去);
(不合题意舍去);
③当 PQ=FQ 时,PH=FH,
∴12﹣3t=6+3t, 解得:t=1;
综上所述,当 t=1 或 t=![]() 时,△PQF 是等腰三角形;
时,△PQF 是等腰三角形;
(3)当折痕经过点 A 时,如图 2 所示:
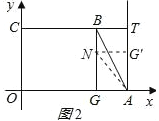
AG=AG′=6,此时 AG′为最大值;
当折痕经过点 B,另一点在 AG 上时 AG′最小,如图 3 所示:
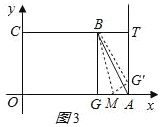
此时,BG=BG′=8,
∵BT=6,
∴在 Rt△BG′T 中, ![]()
∴![]()
综上所述:AG′的最大值与最小值分别是![]()

 名校课堂系列答案
名校课堂系列答案