题目内容
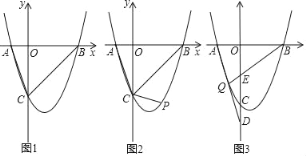
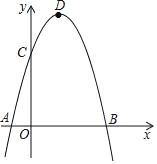
【题目】如图,抛物线y=ax2+bx+c(a<0)与x轴交于A,B两点,与y轴交于点C,点A,顶点D的坐标分别为A(﹣1,0),D(1,m).
(1)当OB=OC时,直接写出抛物线的解析式;
(2)直线CD必经过某一定点,请你分析理由并求出该定点坐标;
(3)点P为直线CD上一点,当以点P,A,B为顶点的三角形是等腰直角三角形时,求m的值.
【答案】(1)y=﹣x2+2x+3;(2)直线CD必经过定点(﹣3,0);(3)以点P,A,B为顶点的三角形是等腰直角三角形时,m的值为2或![]() 或8.
或8.
【解析】
(1)由点A,顶点D的坐标分别为A(﹣1,0),D(1,m),可得B点坐标,又OB=OC,可得抛物线解析式为y=﹣x2+2x+3;
(2)由抛物线顶点D的坐标分别为(1,m),可得b=﹣2a,由A(﹣1,0)在抛物线上,可得c=﹣3a,可得直线CD的解析式为y=﹣ax﹣3a=﹣a(x+3),可得答案;
(3)分 ∠PAB=90°、∠PBA=90°、∠APB=90°三种情况讨论可得m的值.
(1)点A,顶点D的坐标分别为A(﹣1,0),D(1,m),
∴B(3,0),
∴OB=3,
∵OB=OC,
∴C(0,3),
设抛物线解析式为y=a(x+1)(x﹣3),∴a×1×(﹣3)=3,
∴a=﹣1,
∴抛物线解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)∵抛物线顶点D的坐标分别为(1,m),
∴﹣![]() =1,
=1,
∴b=﹣2a,
∴抛物线的解析式为y=ax2﹣2ax+c,
∵A(﹣1,0)在抛物线上,
∴a+2a+c=0,
∴c=﹣3a,
∴抛物线的解析式为y=ax2﹣2ax﹣3a=a(x﹣1)2﹣4a,
∴m=﹣4a,
∴D(1,﹣4a),C(0,﹣3a),
∴直线CD的解析式为y=﹣ax﹣3a=﹣a(x+3),
令x+3=0,
即:x=﹣3时,y=0,
∴直线CD必经过定点(﹣3,0);
(3)A(﹣1,0),B(3,0),
∴AB=4,
当∠PAB=90°时,PA=AB,
∵P(﹣1,﹣2a),
∴PA=﹣2a,
∴﹣2a=4,
∴a=﹣2,
∴m=﹣4a=8
当∠PBA=90°时,PB=AB,
∵P(3,﹣6a),∴PB=﹣6a,
∴﹣6a=4,
∴a=﹣![]() ,
,
∴m=﹣4a=![]() ,
,
当∠APB=90°时,PA=PB,
∵P(1,﹣4a),
∴m=﹣4a=![]() AB=2,
AB=2,
即:以点P,A,B为顶点的三角形是等腰直角三角形时,m的值为2或![]() 或8.
或8.

 阅读快车系列答案
阅读快车系列答案