ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ(1),‘ΎΓςABC÷–,AB=BC,PΈΣAB±Ώ…œ“ΜΒψ,Ν§Ϋ”CP,“‘PAΓΔPCΈΣΝΎ±ΏΉς![]() APCDΘ§AC”κPDœύΫΜ”ΎΒψEΘ§“―÷ΣΓœABC=ΓœAEP=
APCDΘ§AC”κPDœύΫΜ”ΎΒψEΘ§“―÷ΣΓœABC=ΓœAEP=![]() (0Γψ<
(0Γψ<![]() <90Γψ).
<90Γψ).
(1)«σ÷Λ: ΓœEAP=ΓœEPA;
(2)![]() APCD «ΖώΈΣΨΊ–Έ?«κΥΒΟςάμ”…;
APCD «ΖώΈΣΨΊ–Έ?«κΥΒΟςάμ”…;
(3)»γΆΦ(2),FΈΣBC÷–Βψ,Ν§Ϋ”FP,ΫΪΓœAEP»ΤΒψEΥ≥ ±’κ–ΐΉΣ Β±ΒΡΫ«Ε»,ΒΟΒΫΓœMEN(ΒψMΓΔNΖ÷±π «ΓœMENΒΡΝΫ±Ώ”κBAΓΔFP―”≥ΛœΏΒΡΫΜΒψ).≤¬œκœΏΕΈEM”κEN÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έ.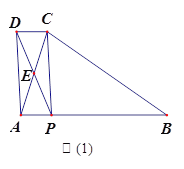
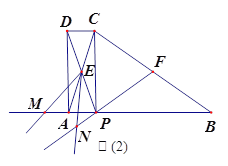
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈωΘΜ
(2)![]() APCD «ΨΊ–Έ.Θ§άμ”…ΦϊΫβΈωΘΜ
APCD «ΨΊ–Έ.Θ§άμ”…ΦϊΫβΈωΘΜ
(3)EM=ENΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίAB=BCΩ…÷ΛΓœCAB=ΓœACBΘ§‘ρ‘ΎΓςABC”κΓςAEP÷–Θ§”–ΝΫΗωΫ«Ε‘”ΠœύΒ»Θ§ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΘ§Φ¥Ω…÷ΛΒΟΘΜ
Θ®2Θ©”…Θ®1Θ©÷ΣΓœEPA=ΓœEAPΘ§‘ρAC=DPΘ§ΗυΨίΕ‘Ϋ«œΏœύΒ»ΒΡΤΫ––ΥΡ±Ώ–Έ «ΨΊ–ΈΦ¥Ω…«σ÷ΛΘΜ
Θ®3Θ©Ω…“‘÷ΛΟςΓςEAMΓ’ΓςEPNΘ§¥”ΕχΒΟΒΫEM=ENΘ°
÷ΛΟςΘΚ(1)‘ΎΓςABCΚΆΓςAEP÷–,
![]() ΓœABC=ΓœAEP,ΓœBAC=ΓœEAP,
ΓœABC=ΓœAEP,ΓœBAC=ΓœEAP,
![]() ΓœACB=ΓœAPE,
ΓœACB=ΓœAPE,
‘ΎΓςABC÷–,AB=BC.![]() ΓœACB=ΓœBAC,
ΓœACB=ΓœBAC,
![]() ΓœEPA=ΓœEAP,
ΓœEPA=ΓœEAP,
(2)![]() APCD «ΨΊ–Έ.
APCD «ΨΊ–Έ.
![]() ΥΡ±Ώ–ΈAPCD «ΤΫ––ΥΡ±Ώ–Έ,
ΥΡ±Ώ–ΈAPCD «ΤΫ––ΥΡ±Ώ–Έ,
![]() AC=2EA,PD=2EP.
AC=2EA,PD=2EP.
”…(1)÷Σ, ΓœEPA=ΓœEAP.
![]() EA=EPΘ§ΫχΕχAC=PD
EA=EPΘ§ΫχΕχAC=PD
![]()
![]() APCD «ΨΊ–Έ.
APCD «ΨΊ–Έ.
(3)EM=EN
![]() EA=EP,
EA=EP,![]() ΓœEPA=90Γψ -
ΓœEPA=90Γψ -![]()
![]() ΓœEAM=180Γψ-ΓœEAP =180Γψ-ΓœEPA= 180Γψ-(90Γψ-
ΓœEAM=180Γψ-ΓœEAP =180Γψ-ΓœEPA= 180Γψ-(90Γψ-![]() )=90Γψ+
)=90Γψ+![]()
”…(2)÷Σ, ΓœCPB=90Γψ,F «BCΒΡ÷–Βψ,![]() FP=FB,
FP=FB,
![]() ΓœFPB=ΓœABC=
ΓœFPB=ΓœABC=![]() Θ§
Θ§
![]() ΓœEPN=ΓœEPA+ΓœAPN=ΓœEPA+ΓœFPB=90Γψ -
ΓœEPN=ΓœEPA+ΓœAPN=ΓœEPA+ΓœFPB=90Γψ -![]() +
+![]() =90Γψ+
=90Γψ+![]()
![]() ΓœEAM=ΓœEPN
ΓœEAM=ΓœEPN
![]() ΓœAEP»ΤΒψEΥ≥ ±’κ–ΐΉΣ Β±ΒΡΫ«Ε»Θ§ΒΟΒΫΓœMENΘ§
ΓœAEP»ΤΒψEΥ≥ ±’κ–ΐΉΣ Β±ΒΡΫ«Ε»Θ§ΒΟΒΫΓœMENΘ§
![]() ΓœAEP-ΓœAEN =ΓœMEN-ΓœAEN,Φ¥ΓœMEA=ΓœNEP.
ΓœAEP-ΓœAEN =ΓœMEN-ΓœAEN,Φ¥ΓœMEA=ΓœNEP.
![]() ΓςEAMΓ’ΓςEPN,
ΓςEAMΓ’ΓςEPN,
![]() EM=EN.
EM=EN.

 –«ΦΕΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗ
–«ΦΕΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗ ΟΔΙϊΫΧΗ®¥ο±ξ≤β ‘ΨμœΒΝ–¥πΑΗ
ΟΔΙϊΫΧΗ®¥ο±ξ≤β ‘ΨμœΒΝ–¥πΑΗ