Question

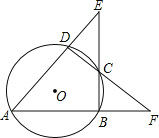
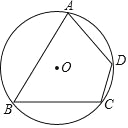
【题目】（8分）如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．

（1）若∠E=∠F时，求证：∠ADC=∠ABC；

（2）若∠E=∠F=42°时，求∠A的度数；

（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．

Answer 1

【答案】（1）见解析；（2）48°；（3）∠A=90°﹣．

【解析】

试题（1）根据外角的性质即可得到结论；

（2）根据圆内接四边形的性质和等量代换即可求得结果；

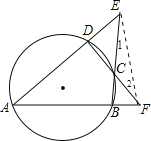
（3）连结EF，如图，根据圆内接四边形的性质得∠ECD=∠A，再根据三角形外角性质得∠ECD=∠1+∠2，则∠A=∠1+∠2，然后根据三角形内角和定理有∠A+∠1+∠2+∠E+∠F=180°，即2∠A+α+β=180°，再解方程即可．

试题解析：解：（1）∠E=∠F，

∵∠DCE=∠BCF，

∴∠ADC=∠E+∠DCE，∠ABC=∠F+∠BCF，

∴∠ADC=∠ABC；

（2）由（1）知∠ADC=∠ABC，

∵∠EDC=∠ABC，

∴∠EDC=∠ADC，

∴∠ADC=90°，

∴∠A=90°﹣42°=48°；

（3）连结EF，如图，

∵四边形ABCD为圆的内接四边形，

∴∠ECD=∠A，

∵∠ECD=∠1+∠2，

∴∠A=∠1+∠2，

∵∠A+∠1+∠2+∠E+∠F=180°，

∴2∠A+α+β=180°，

∴∠A=90°﹣．