Question

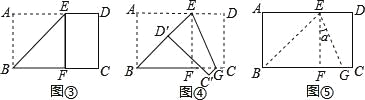
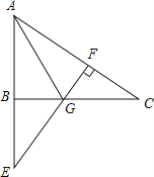
【题目】如图，在Rt△ABC中，∠ABC=90°，延长AB至E，使AE=AC，过E作EF⊥AC于F，EF交BC于G．

（1）求证：BE=CF；

（2）若∠E=40°，求∠AGB的度数．

Answer 1

【答案】（1）证明见解析；（2）∠AGB=65°．

【解析】

（1）首先证明△ABC△AFE，推出AB=AF，即可解决问题．

（2）在Rt△BEG中，∠BGE=90°-∠E=50°，推出∠BGF=130°，由Rt△AGFRt△AGB，推出∠AGB=∠AGF=∠BGF即可解决问题．

证明：（1）∵∠ABC=90°，EF⊥AC，

∴∠ABC=∠AFE=90°

在△AEF与△ACB中

，

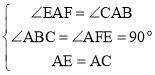∴△AEF△ACB（AAS）

∴AF=AB，

∴BE=CF；

（2）∵△ABC△AFE，

∴AB=AF，

在Rt△AGF和Rt△AGB中，

∴Rt△AFGRt△ABG（HL）

在Rt△BEG中，∠BGE=90°-∠E=50°，

∴∠BGF=130°，

∵Rt△AGFRt△AGB，

∴∠AGB=∠AGF=∠BGF=65°．