��Ŀ����
����Ŀ����2015ɽ��ʡ�����У�24��12�֣���֪������y=-mx2+4x+2m��x�ύ�ڵ�A������0���� B������0������![]() ��
��
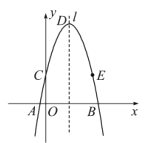
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ���Ϊl����y��Ľ���ΪC������ΪD����C����l�ĶԳƵ�ΪE���Ƿ����x���ϵĵ�M��y���ϵĵ�N��ʹ�ı���DNME���ܳ���С�������ڣ��뻭��ͼ�Σ�������ͼ�ۼ�����������ܳ�����Сֵ���������ڣ���˵�����ɣ�
��3������P���������ϣ���Q��x���ϣ����Ե�D��E��P��QΪ������ı�����ƽ���ı���ʱ�����P�����꣮
���𰸡���1��y=-x2+4x+2��
��2���ı���DNME���ܳ�����СֵΪ10+2![]()
��3����2-![]() ��4������2+
��4������2+![]() ��4������2+
��4������2+![]() ��-4������2-
��-4������2-![]() ��-4����
��-4����
��������
���⣨1�����ø�����ϵ���Ĺ�ϵ�ó���+��=![]() ������=��2�������������m��ֵ���ɵó��𰸣�
������=��2�������������m��ֵ���ɵó��𰸣�
��2��������Գ������·�ߵķ���������D����y��ĶԳƵ�D������E����x��ĶԳƵ�E�����ó��ı���DNME���ܳ���СΪ��D��E��+DE���������ù��ɶ���������ɣ�
��3������ƽ���ı��ε��ж������ʽ��P��������Ϊ��4�������ֱ�������ɣ�
�⣺��1��������ɵã��������Ƿ�����mx2+4x+2m=0���������ɸ���ϵ���Ĺ�ϵ�ɵã�
��+��=![]() ������=��2��
������=��2��
��![]() =��2��
=��2��
��![]() =��2����
=��2����![]() =��2��
=��2��
��ã�m=1��
�������߽���ʽΪ��y=��x2+4x+2��
��2������x���ϵĵ�M��y���ϵĵ�N��ʹ���ı���DNME���ܳ���С��
��y=��x2+4x+2=����x��2��2+6��
�������ߵĶԳ���lΪx=2������D������Ϊ����2��6����
������������y�ύ��C������Ϊ����0��2������E���C����l�Գƣ�
��E����������4��2����
����D����y��ĶԳƵ�D������E����x��ĶԳƵ�E����
��D��������������2��6����E����������4����2����
����D��E������x����M����y����N��
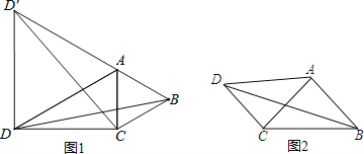
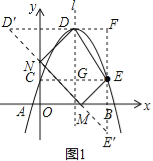
��ʱ���ı���DNME���ܳ���СΪ��D��E��+DE����ͼ1��ʾ��
�ӳ�E��E����D����һ��F����Rt��D��E��F�У�D��F=6��E��F=8��
��D��E��=![]() =
=![]() =10��
=10��
��Գ���l��CE���ڵ�G����Rt��DGE�У�DG=4��EG=2��
��DE=![]() =
=![]() =2
=2![]() ��
��
���ı���DNME���ܳ���СֵΪ��10+2![]() ��
��
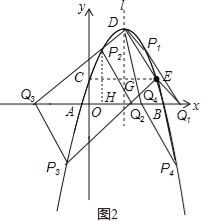
��3����ͼ2��PΪ�������ϵĵ㣬����P��PH��x�ᣬ����ΪH��
���Ե�D��E��P��QΪ������ı���Ϊƽ���ı��Σ�����PHQ�ա�DGE��
��PH=DG=4��
��|y|=4��
����y=4ʱ����x2+4x+2=4��
��ã�x1=2+![]() ��x2=2��
��x2=2��![]() ��
��
��y=��4ʱ����x2+4x+2=��4��
��ã�x3=2+![]() ��x4=2��
��x4=2��![]() ��
��
��P�����������2��![]() ��4������2+
��4������2+![]() ��4������2��
��4������2��![]() ����4������2+
����4������2+![]() ����4����
����4����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�