Question

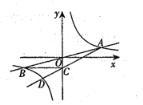
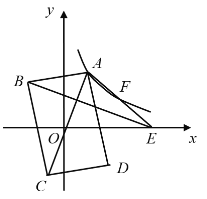
【题目】如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE．若AD平分，反比例函数的图象经过AE上的两点A，F，且，的面积为18，则k的值为（ ）

A.6B.12C.18D.24

Answer 1

【答案】B

【解析】

先证明OB∥AE，得出S△ABE=S△OAE=18，设A的坐标为（a，），求出F点的坐标和E点的坐标，可得S△OAE=×3a×=18，求解即可．

解：如图，连接BD，

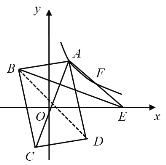
∵四边形ABCD为矩形，O为对角线，

∴AO=OD，

∴∠ODA=∠OAD，

又∵AD为∠DAE的平分线，

∴∠OAD=∠EAD，

∴∠EAD=∠ODA，

∴OB∥AE，

∵S△ABE=18，

∴S△OAE=18，

设A的坐标为（a，），

∵AF=EF，

∴F点的纵坐标为，

代入反比例函数解析式可得F点的坐标为（2a，），

∴E点的坐标为（3a，0），

S△OAE=×3a×=18，

解得k=12，

故选：B．