Question

【题目】设等边三角形的内切圆半径为外接圆半径为，平面内任意一点到等边三角形中心的距离为若满足则称点叫做等边三角形的中心关联点．在平面直角坐标系中，等边的三个顶点的坐标分别为．

（1）①等边中心的坐标为 ；

②已知点在中，是等边的中心关联点的是 ；

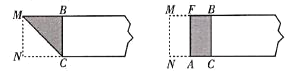
（2）如图1，过点作直线交轴正半轴于使．

　　

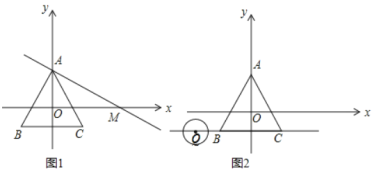
①若线段上存在等边的中心关联点求的取值范围；

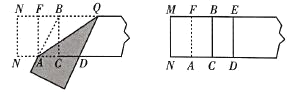
②将直线向下平移得到直线当满足什么条件时，直线上总存在等边的中心关联点；

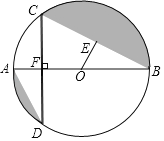
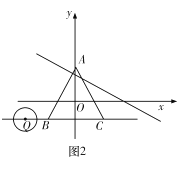
（3）如图2，点为直线上一动点，的半径为当从点出发，以每秒个单位的速度向右移动，运动时间为秒．是否存在某一时刻使得上所有点都是等边的中心关联点？如果存在，请直接写出所有符合题意的的值；如果不存在，请说明理由．

Answer 1

【答案】（1）①；②；（2）①，②满足条件的的值为；（3）存在. 或．

【解析】

（1）①求出OA＝OB＝OC＝2，即可得等边中心的坐标；

②分别求出OD，OE，OF，然后根据中心关联点的定义判断；

（2）①易得直线的解析式，判断出点在直线AM上，根据点P在AE上时，可得此时点P都是等边△ABC的中心关联点；

②如图1-2中，设平移后的直线交轴于点，过点作这条直线的垂线，垂足为，求出时OG的长，即可得到b的取值范围；

（3）如图2中，设Q（s，1），由题意得当OQ＝时，⊙Q上所有点都是等边△ABC的中心关联点，求出s即可得解．

解：（1）①∵，

∴OA＝2，OB＝，OC＝，

∴等边中心的坐标为；

②由题意得：，点是的中心，

，

点是的中心关联点；

（2）①如图1-1中，

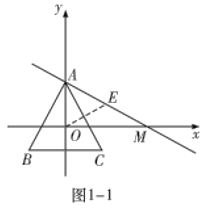
∵OA＝2，，

∴OM＝，

易得直线的解析式为：，

∴在直线上，

因为，

所以为等边三角形，

所以边上的高长为，

当点在上时，，

所以当点在上时，点都是等边的中心关联点，

所以；

如图1-2中，设平移后的直线交轴于点过点作这条直线的垂线，垂足为，

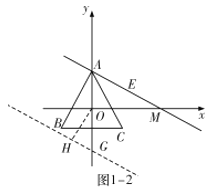
当时，在中，，

，

，

满足条件的的值为；

存在，

理由：如图2中，设，

由题意得，当时，上所有点都是等边的中心关联点，

∴，

解得：，

或．