题目内容
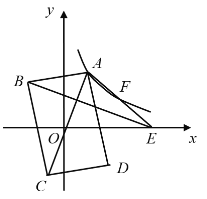
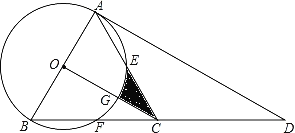
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:DE是⊙O的切线;
(2)若∠BAC=30°,AB=12,求阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接DB,根据圆周角定理、直角三角形的性质证明;
(2)根据扇形面积公式计算即可.
(1)证明:连接DB,
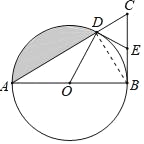
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,
∵点E是BC的中点,
∴DE=CE=![]() BC,
BC,
∴∠EDC=∠C,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠ADO+∠EDC=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)∵AB=12,∠BAC=30°,
∴AD=6![]() ,
,
阴影部分的面积=![]() ﹣
﹣![]() ×6×3
×6×3![]() =12π﹣9
=12π﹣9![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )的
)的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
| 0 | 2 |
| 6 | 0 |
|
| 6 |
下列结论:
①![]() ;
;
②当![]() 时,函数最小值为
时,函数最小值为![]() ;
;
③若点![]() ,点
,点![]() 在二次函数图象上,则
在二次函数图象上,则![]() ;
;
④方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)