题目内容
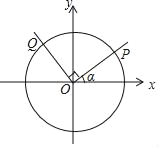
【题目】一般地,我们把半径为1的圆叫做单位圆,在平面直角坐标系xOy中,设单位圆的圆心与坐标原点O重合,则单位圆与x轴的交点分别为(1,0),(﹣1,0),与y轴的交点分别为(0,1),(0,﹣1).在平面直角坐标系xOy中,设锐角α的顶点与坐标原点O重合,α的一边与x轴的正半轴重合,另一边与单位圆交于点P(x1,y1),且点P在第一象限.
(1)求x1(用含α的式子表示);y1(用含α的式子表示);
(2)将射线OP绕坐标原点O按逆时针方向旋转90°后与单位圆交于点Q(x2,y2).
①判断y1与x2的数量关系,并证明;
②写出y1+y2的取值范围.
【答案】(1)cosα,sinα;(2)①结论:y1=﹣x2.理由解析;②1<y1+y2≤![]() .
.
【解析】
(1)如图作PF⊥x轴于F,QE⊥x轴于E.则OF=OPcosα,PF=OPsinα,由此即可解决问题;
(2)①过点P作PF⊥x轴于点F,过点Q作QE⊥x轴于点E.只要证明△QOE≌△OPF即可解决问题;
②当P在x轴上时,得到y1+y2的最小值为1,由y1+y2=PF+QE=OE+OF=EF,四边形QEFP是直角梯形,PQ=![]() ,EF≤PQ,即可推出当EF=PQ=
,EF≤PQ,即可推出当EF=PQ=![]() 时,得到y1+y2的最大值为
时,得到y1+y2的最大值为![]() .
.
(1)如图作PF⊥x轴于F,则∠OFP=90°,PF=y1,OF=x1,
在Rt△OFP中,sinα=![]() ,cosα=
,cosα=![]() ,
,
∴OF=OPcosα,PF=OPsinα,
又∵OP=1,
∴x1=cosα,y1=sinα;
(2)①结论:y1=﹣x2.
理由:过点P作PF⊥x轴于点F,过点Q作QE⊥x轴于点E.
∴∠PFO=∠QEO=∠POQ=90°,
∴∠POF+∠OPF=90°,∠POF+∠QOE=90°,
∴∠QOE=∠OPF,
∵OQ=OP,
∴△QOE≌△OPF,
∴PF=OE,
∵P(x1,y1),Q(x2,y2),
∴PF=y1,OE=﹣x2,
∴y1=﹣x2
②当P在x轴上时,得到y1+y2的最小值为1,
∵y1+y2=PF+QE=OE+OF=EF,
∵四边形QEFP是直角梯形,PQ=![]() ,EF≤PQ,
,EF≤PQ,
∴当EF=PQ=![]() 时,得到y1+y2的最大值为
时,得到y1+y2的最大值为![]() ,
,
∴1<y1+y2≤![]() ,
,
故答案为1<y1+y2≤![]() .
.