Question

【题目】已知：如图，△ABC中，P、Q两点分别是边AB和AC的垂直平分线与BC的交点，连结AP和AQ，且BP＝PQ＝QC．求∠C的度数．

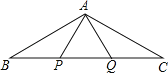
证明：∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点，

∴PA＝　 　，QC＝QA．　 　

∵BP＝PQ＝QC，

∴在△APQ中，PQ＝　 　（等量代换）

∴△APQ是　 　三角形．

∴∠AQP＝60°，

∵在△AQC中，QC＝QA，

∴∠C＝∠　 　．

又∵∠AQP是△AQC的外角，

∴∠AQP＝∠　 　+∠　 　＝60°．（三角形的一个外角等于与它不相邻的两个内角的和）

∴∠C＝　 　．

Answer 1

【答案】BP，垂直平分线上任意一点，到线段两端点的距离相等，PA＝QA，等边，QAC，C，QAC，30°．

【解析】

根据线段垂直平分线的性质可得PA＝BP，QC＝QA，再根据等量关系可得PQ＝PA＝QA，可得△APQ是 等边三角形，根据等边三角形的性质可得∠AQP＝60°，再根据三角形三角形外角的性质和等腰的性质可求∠C的度数．

解：证明：∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点，

∴PA＝BP，QC＝QA．（垂直平分线上任意一点，到线段两端点的距离相等）

∵BP＝PQ＝QC，

∴在△APQ中，PQ＝PA＝QA（等量代换）

∴△APQ是等边三角形．

∴∠AQP＝60°，

∵在△AQC中，QC＝QA，

∴∠C＝∠QAC．

又∵∠AQP是△AQC的外角，

∴∠AQP＝∠C+∠QAC＝60°．

（三角形的一个外角等于与它不相邻的两个内角的和）

∴∠C＝30°．

故答案为：BP，（垂直平分线上任意一点，到线段两端点的距离相等），PA＝QA，等边，QAC，C，QAC，30°．