题目内容
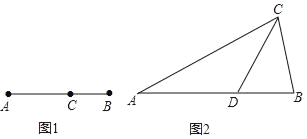
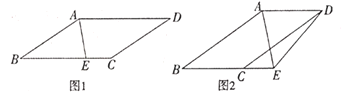
【题目】如图,已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
【答案】(1)详见解析;(2)135°
【解析】
(1)根据平行线的性质求出∠DAE=∠BEA,由AE平分∠BAD得∠BAE=∠DAE,从而得出结论.(2)由根据∠ADE=3∠CDE设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程![]() ,求出x即可.
,求出x即可.
(1)证明:∵AB∥CD,
∴∠B+∠C=180°.
∵∠B=∠D,
∴∠C+∠D=180
∴AD∥BC.
∴∠DAE=∠BEA.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠BAE=∠BEA.
(2)解:∵∠ADE=3∠CDE,设∠CDE=x,
∴∠ADE=3x,∠ADC=2x.
∵AB∥CD,
∴∠BAD+∠ADC=180
∴![]()
由(1)可知:![]() ,
,
∵AD∥BC
∴∠BED+∠ADE=180°
∴![]()
∵∠AED=60°,
即![]() ,
,
∴∠CDE=x=15°,∠ADE=45°.
∵AD∥BC.
∴![]() .
.

练习册系列答案
相关题目